sfepy.terms.terms_basic module¶

class sfepy.terms.terms_basic.IntegrateMatTerm(name, arg_str, integral, region, **kwargs)[source]¶

Evaluate material parameter 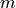$m$ in a volume region.

Depending on evaluation mode, integrate a material parameter over a volume region (‘eval’), average it in elements (‘el_avg’) or interpolate it into volume quadrature points (‘qp’).

Uses reference mapping of 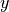$y$ variable.

Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.

Definition:

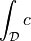
$\int_{\cal{D}} c$

Call signature:

ev_integrate_mat

(material, parameter)

Arguments:

material : $c$ (can have up to two dimensions)
parameter : $y$

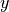
arg_shapes = [{'material': 'N, N', 'parameter': 'N'}]¶

arg_types = ('material', 'parameter')¶

static function(out, mat, geo, fmode)[source]¶

get_eval_shape(mat, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = ('cell', 'facet')¶

name = 'ev_integrate_mat'¶

class sfepy.terms.terms_basic.IntegrateOperatorTerm(name, arg_str, integral, region, **kwargs)[source]¶

Integral of a test function weighted by a scalar function $c$ .

Definition:

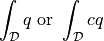
$\int_{\cal{D}} q \mbox{ or } \int_{\cal{D}} c q$

Call signature:

dw_integrate

(opt_material, virtual)

Arguments:

material : $c$ (optional)
virtual : $q$

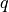
arg_shapes = [{'opt_material': '1, 1', 'virtual': (1, None)}, {'opt_material': None}]¶

arg_types = ('opt_material', 'virtual')¶

static function(out, material, bf, geo)[source]¶

get_fargs(material, virtual, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = ('cell', 'facet')¶

name = 'dw_integrate'¶

class sfepy.terms.terms_basic.IntegrateTerm(name, arg_str, integral, region, **kwargs)[source]¶

Evaluate (weighted) variable in a region.

Depending on evaluation mode, integrate a variable over a region (‘eval’), average it in elements (‘el_avg’) or interpolate it into quadrature points (‘qp’). For a surface region and vector variables, setting term_mode to ‘flux’ leads to computing corresponding fluxes for the three modes instead.

Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.

Definition:

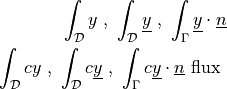
$\int_{\cal{D}} y \mbox{ , } \int_{\cal{D}} \ul{y} \mbox{ , } \int_\Gamma \ul{y} \cdot \ul{n}\\ \int_{\cal{D}} c y \mbox{ , } \int_{\cal{D}} c \ul{y} \mbox{ , } \int_\Gamma c \ul{y} \cdot \ul{n} \mbox{ flux }$

Call signature:

ev_integrate

(opt_material, parameter)

Arguments:

material : $c$ (optional)
parameter : 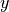$y$ or $\ul{y}$

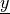
arg_shapes = [{'opt_material': '1, 1', 'parameter': 'N'}, {'opt_material': None}]¶

arg_types = ('opt_material', 'parameter')¶

static function(out, val_qp, vg, fmode)[source]¶

get_eval_shape(material, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(material, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = ('cell', 'facet')¶

name = 'ev_integrate'¶

class sfepy.terms.terms_basic.SumNodalValuesTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sum nodal values.

Call signature:

ev_sum_vals

(parameter)

Arguments:

parameter : $p$ or $\ul{u}$

arg_shapes = {'parameter': 'N'}¶

arg_types = ('parameter',)¶

static function(out, vec)[source]¶

get_eval_shape(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sum_vals'¶

class sfepy.terms.terms_basic.SurfaceMomentTerm(name, arg_str, integral, region, **kwargs)[source]¶

Surface integral of the outer product of the unit outward normal 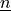$\ul{n}$ and the coordinate 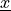$\ul{x}$ shifted by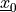 $\ul{x}_0$

Definition:

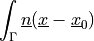
$\int_{\Gamma} \ul{n} (\ul{x} - \ul{x}_0)$

Call signature:

ev_surface_moment

(material, parameter)

Arguments:

material : 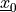$\ul{x}_0$ (special)
parameter : any variable

arg_shapes = {'material': '.: D', 'parameter': 'N'}¶

arg_types = ('material', 'parameter')¶

static function(out, in_, cmap, conn)¶

get_eval_shape(material, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(material, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = 'facet'¶

name = 'ev_surface_moment'¶

class sfepy.terms.terms_basic.VolumeSurfaceTerm(name, arg_str, integral, region, **kwargs)[source]¶

Volume of a 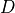$D$ -dimensional domain, using a surface integral. Uses approximation of the parameter variable.

Definition:

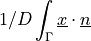
$1 / D \int_\Gamma \ul{x} \cdot \ul{n}$

Call signature:

ev_volume_surface

(parameter)

Arguments:

parameter : any variable

arg_shapes = {'parameter': 'N'}¶

arg_types = ('parameter',)¶

static function(out, in_, cmap, conn)¶

get_eval_shape(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = 'facet'¶

name = 'ev_volume_surface'¶

class sfepy.terms.terms_basic.VolumeTerm(name, arg_str, integral, region, **kwargs)[source]¶

Volume or surface of a domain. Uses approximation of the parameter variable.

Definition:

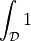
$\int_{\cal{D}} 1$

Call signature:

ev_volume

(parameter)

Arguments:

parameter : any variable

arg_shapes = [{'parameter': 'N'}]¶

arg_types = ('parameter',)¶

static function(out, geo)[source]¶

get_eval_shape(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = ('cell', 'facet')¶

name = 'ev_volume'¶

class sfepy.terms.terms_basic.ZeroTerm(name, arg_str, integral, region, **kwargs)[source]¶

A do-nothing term useful for introducing additional variables into the equations.

Definition:

$0$

Call signature:

dw_zero

(virtual, state)

Arguments:

virtual : 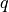$q$ or $\ul{v}$
state : $p$ or $\ul{u}$

arg_shapes = {'state': 'N', 'virtual': ('N', None)}¶

arg_types = ('virtual', 'state')¶

static function(out)[source]¶

get_fargs(vvar, svar, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_zero'¶