sfepy.mechanics.tensors module¶
Functions to compute some tensor-related quantities usual in continuum mechanics.
- class sfepy.mechanics.tensors.StressTransform(def_grad, jacobian=None)[source]¶
Encapsulates functions to convert various stress tensors in the symmetric storage given the deformation state.
- get_1pk_from_2pk(stress_in)[source]¶
Get the first Piola-Kirchhoff stress given the second Piola-Kirchhoff stress.
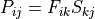
- Parameters:
- stress_inarray_like
The second Piola-Kirchhoff stress in vector symmetric storage with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png)
- Returns:
- stress_out_fullarray
The first Piola-Kirchhoff stress in matrix storage.
- get_cauchy_from_2pk(stress_in)[source]¶
Get the Cauchy stress given the second Piola-Kirchhoff stress.
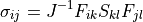
- Parameters:
- stress_inarray_like
The second Piola-Kirchhoff stress in vector symmetric storage with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png)
- Returns:
- stress_outarray
The Cauchy stress in vector symmetric storage with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) .
.
- sfepy.mechanics.tensors.dim2sym(dim)[source]¶
Given the space dimension, return the symmetric storage size.
- sfepy.mechanics.tensors.get_cauchy_strain(grad)[source]¶
Given a gradient, return the corresponding Cauchy strain (symmetric gradient).
- sfepy.mechanics.tensors.get_deviator(tensor, sym_storage=True)[source]¶
The deviatoric part (deviator) of a tensor.
- sfepy.mechanics.tensors.get_full_indices(dim)[source]¶
The indices for converting the symmetric storage to the full storage.
- sfepy.mechanics.tensors.get_non_diagonal_indices(dim)[source]¶
The non_diagonal indices for the full vector storage.
- sfepy.mechanics.tensors.get_sym_indices(dim)[source]¶
The indices for converting the full storage to the symmetric storage.
- sfepy.mechanics.tensors.get_t4_from_t2s(t2s)[source]¶
Get the full 4D tensor with major/minor symmetries from its 2D matrix representation.
- Parameters:
- t2sarray
The symmetrically-stored tensor of shape (S, S), where S it the symmetric storage size.
- Returns:
- t4array
The full 4D tensor of shape (D, D, D, D), where D is the space dimension.
- sfepy.mechanics.tensors.get_volumetric_tensor(tensor, sym_storage=True)[source]¶
The volumetric part of a tensor.
- sfepy.mechanics.tensors.get_von_mises_stress(stress, sym_storage=True)[source]¶
Given a symmetric stress tensor, compute the von Mises stress (also known as Equivalent tensile stress).
Notes

- sfepy.mechanics.tensors.prepare_cylindrical_transform(coors, origin, mode='axes')[source]¶
Prepare matrices for transforming tensors into cylindrical coordinates with the axis ‘z’ in a given origin.
- Parameters:
- coorsarray
The Cartesian coordinates.
- originarray of length 3
The origin.
- mode‘axes’ or ‘data’
In ‘axes’ (default) mode the matrix transforms data to different coordinate system, while in ‘data’ mode the matrix transforms the data in the same coordinate system and is transpose of the matrix in the ‘axes’ mode.
- Returns:
- mtxarray
The array of transformation matrices for each coordinate in coors.
- sfepy.mechanics.tensors.sym2dim(sym)[source]¶
Given the symmetric storage size, return the space dimension.
Notes
This function works for any space dimension.
- sfepy.mechanics.tensors.transform_data(data, coors=None, mode='cylindrical', mtx=None)[source]¶
Transform vector or tensor data components between orthogonal coordinate systems in 3D using transformation matrix
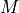 , that
should express rotation of the original coordinate system to the new
system denoted by
, that
should express rotation of the original coordinate system to the new
system denoted by  below.
below.For vectors:
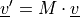
For second order tensors:
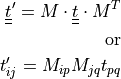
For fourth order tensors:
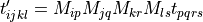
- Parameters:
- dataarray, shape (num, n_r) or (num, n_r, n_c)
The vectors (n_r is 3) or tensors (symmetric storage, n_r is 6, n_c, if available, is 1 or 6) to be transformed.
- coorsarray
The Cartesian coordinates of the data. Not needed when mtx argument is given.
- modeone of [‘cylindrical’]
The requested coordinate system. Not needed when mtx argument is given.
- mtxarray
The array of transformation matrices
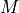 for each data row.
for each data row.
- Returns:
- new_dataarray
The transformed data.