sfepy.mechanics.shell10x module¶
Functions implementing the shell10x element.
- sfepy.mechanics.shell10x.add_eas_dofs(mtx_b, qp_coors, det, det0, dxidx0)[source]¶
Add additional strain components [Andelfinger and Ramm] (7 parameters to be condensed out).
- sfepy.mechanics.shell10x.create_drl_transform(ebs)[source]¶
Create the transformation matrix for locking of the drilling rotations.
- sfepy.mechanics.shell10x.create_elastic_tensor(young, poisson, shear_correction=True)[source]¶
Create the elastic tensor with the applied shear correction (the default) for the shell10x element.
- sfepy.mechanics.shell10x.create_local_bases(coors)[source]¶
Create local orthonormal bases in each vertex of quadrilateral cells.
- Parameters:
- coorsarray
The coordinates of cell vertices, shape (n_el, 4, 3).
- Returns:
- ebsarray
The local bases, shape (n_el, 4, 3, 3). The basis vectors are rows of the (…, 3, 3) blocks.
- sfepy.mechanics.shell10x.create_rotation_ops(ebs)[source]¶
Create operators associated to rotation DOFs.
- Parameters:
- ebsarray
The local bases, shape (n_el, 4, 3, 3).
- Returns:
- ropsarray
The rotation operators, shape (n_el, 4, 3, 3).
- sfepy.mechanics.shell10x.create_strain_matrix(bfgm, dxidx, dsg)[source]¶
Create the strain operator matrix.
- sfepy.mechanics.shell10x.create_strain_transform(mtx_ts)[source]¶
Create strain tensor transformation matrices, given coordinate transformation matrices.
Notes
Expresses
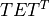 in terms of symmetrix storage as
in terms of symmetrix storage as 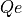 ,
with the ordering of components:
,
with the ordering of components:
![e = [e_{11}, e_{22}, e_{33}, 2 e_{12}, 2 e_{13}, 2 e_{23}]](../../../_images/math/c77a7acc7db139080a46a7db935e63f8c43a3286.png) .
.
- sfepy.mechanics.shell10x.create_transformation_matrix(coors)[source]¶
Create a transposed coordinate transformation matrix, that transforms 3D coordinates of quadrilateral cell vertices so that the transformed vertices of a plane cell are in the
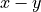 plane. The rotation is performed
w.r.t. the centres of quadrilaterals.
plane. The rotation is performed
w.r.t. the centres of quadrilaterals.- Parameters:
- coorsarray
The coordinates of cell vertices, shape (n_el, 4, 3).
- Returns:
- mtx_tarray
The transposed transformation matrix
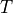 , i.e.
, i.e.
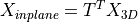 .
.
Notes
![T = [t_1, t_2, n]](../../../_images/math/4fff2b5da6da8807bad080ad935b16c2d65caf96.png) , where
, where 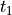 ,
, 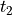 , are unit
in-plane (column) vectors and
, are unit
in-plane (column) vectors and 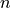 is the unit normal vector,
all mutually orthonormal.
is the unit normal vector,
all mutually orthonormal.
- sfepy.mechanics.shell10x.get_dsg_strain(coors_loc, qp_coors)[source]¶
Compute DSG strain components.
- Returns:
- dsgarray
The strain matrix components corresponding to
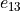 ,
,
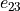 , shape (n_el, n_qp, 2, 24).
, shape (n_el, n_qp, 2, 24).
Notes
Involves
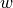 ,
, 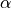 ,
, 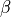 DOFs.
DOFs.
- sfepy.mechanics.shell10x.get_mapping_data(ebs, rops, ps, coors_loc, qp_coors, qp_weights, special_dx3=False)[source]¶
Compute reference element mapping data for shell10x elements.
Notes
The code assumes that the quadrature points are w.r.t. (
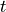 =
thickness of the shell)
=
thickness of the shell) ![[0, 1] \times [0, 1] \times [-t/2, t/2]](../../../_images/math/9268a3b52238a10d61dd3b0622390c46c6188cbd.png) reference cell and the quadrature weights are multiplied by
reference cell and the quadrature weights are multiplied by 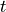 .
.
- sfepy.mechanics.shell10x.lock_drilling_rotations(mtx, ebs, coefs)[source]¶
Lock the drilling rotations in the stiffness matrix.
- sfepy.mechanics.shell10x.rotate_elastic_tensor(mtx_d, bfu, ebs)[source]¶
Rotate the elastic tensor into the local coordinate system of each cell. The local coordinate system results from interpolation of ebs with the bilinear basis.
- sfepy.mechanics.shell10x.transform_asm_matrices(out, mtx_t, blocks)[source]¶
Transform matrix assembling contributions to global coordinate system, one node at a time.
- Parameters:
- outarray
The array of matrices, transformed in-place.
- mtx_tarray
The array of transposed transformation matrices
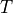 , see
, see
create_transformation_matrix().- blocksarray
The DOF blocks that are