sfepy.terms.terms_elastic module¶
- class sfepy.terms.terms_elastic.CauchyStrainTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate Cauchy strain tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22,
12]](../../../_images/math/8463e6b27c080a6b17a11e11ed7bcbef831264c9.png) . The last three (non-diagonal) components are doubled so that it is
energetically conjugate to the Cauchy stress tensor with the same storage.
. The last three (non-diagonal) components are doubled so that it is
energetically conjugate to the Cauchy stress tensor with the same storage.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
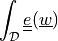
- Call signature:
ev_cauchy_strain
(parameter)- Arguments:
parameter :
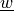
- arg_shapes = {'parameter': 'D'}¶
- arg_types = ('parameter',)¶
- integration = ('cell', 'facet_extra')¶
- name = 'ev_cauchy_strain'¶
- class sfepy.terms.terms_elastic.CauchyStressETHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate fading memory Cauchy stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Assumes an exponential approximation of the convolution kernel resulting in much higher efficiency.
Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
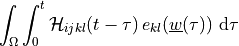
- Call signature:
ev_cauchy_stress_eth
(ts, material_0, material_1, parameter)- Arguments:
ts :
TimeStepperinstancematerial_0 :
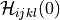
material_1 :
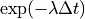 (decay at
(decay at 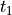 )
)parameter :
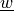
- arg_shapes = {'material_0': 'S, S', 'material_1': '1, 1', 'parameter': 'D'}¶
- arg_types = ('ts', 'material_0', 'material_1', 'parameter')¶
- get_eval_shape(ts, mat0, mat1, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'ev_cauchy_stress_eth'¶
- class sfepy.terms.terms_elastic.CauchyStressTHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate fading memory Cauchy stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
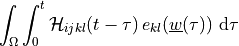
- Call signature:
ev_cauchy_stress_th
(ts, material, parameter)- Arguments:
ts :
TimeStepperinstancematerial :
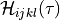
parameter :
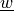
- arg_shapes = {'material': '.: N, S, S', 'parameter': 'D'}¶
- arg_types = ('ts', 'material', 'parameter')¶
- name = 'ev_cauchy_stress_th'¶
- class sfepy.terms.terms_elastic.CauchyStressTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate Cauchy stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:

- Call signature:
ev_cauchy_stress
(material, parameter)- Arguments:
material :
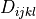
parameter :
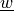
- arg_shapes = {'material': 'S, S', 'parameter': 'D'}¶
- arg_types = ('material', 'parameter')¶
- integration = ('cell', 'facet_extra')¶
- name = 'ev_cauchy_stress'¶
- class sfepy.terms.terms_elastic.ElasticWaveCauchyTerm(name, arg_str, integral, region, **kwargs)[source]¶
Elastic dispersion term involving the wave strain
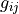 ,
,
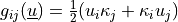 , with the
wave vector
, with the
wave vector 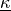 and the elastic strain
and the elastic strain 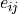 .
.
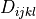 is given in the usual matrix form exploiting symmetry: in
3D it is
is given in the usual matrix form exploiting symmetry: in
3D it is 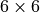 with the indices ordered as
with the indices ordered as ![[11, 22, 33,
12, 13, 23]](../../../_images/math/c9b16ea0f2338a14e35327dda57164b08229a665.png) , in 2D it is
, in 2D it is 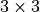 with the indices ordered as
with the indices ordered as
![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.- Definition:
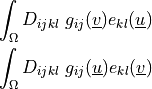
- Call signature:
dw_elastic_wave_cauchy
(material_1, material_2, virtual, state)(material_1, material_2, state, virtual)- Arguments 1:
material_1 :
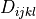
material_2 :
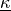
virtual :

state :

- Arguments 2:
material_1 :
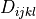
material_2 :
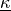
state :

virtual :

- arg_shapes = {'material_1': 'S, S', 'material_2': '.: D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material_1', 'material_2', 'virtual', 'state'), ('material_1', 'material_2', 'state', 'virtual'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- modes = ('ge', 'eg')¶
- name = 'dw_elastic_wave_cauchy'¶
- class sfepy.terms.terms_elastic.ElasticWaveTerm(name, arg_str, integral, region, **kwargs)[source]¶
Elastic dispersion term involving the wave strain
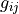 ,
,
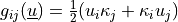 , with the
wave vector
, with the
wave vector 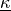 .
. 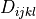 is given in the usual
matrix form exploiting symmetry: in 3D it is
is given in the usual
matrix form exploiting symmetry: in 3D it is 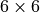 with the
indices ordered as
with the
indices ordered as ![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in 2D it is
, in 2D it is
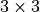 with the indices ordered as
with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.- Definition:
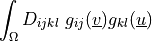
- Call signature:
dw_elastic_wave
(material_1, material_2, virtual, state)- Arguments:
material_1 :
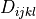
material_2 :
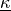
virtual :

state :

- arg_shapes = {'material_1': 'S, S', 'material_2': '.: D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_1', 'material_2', 'virtual', 'state')¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- name = 'dw_elastic_wave'¶
- class sfepy.terms.terms_elastic.LinearDRotSpringTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear spring element with the stiffness transformed into the element direction.
- Definition:
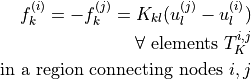
- Call signature:
dw_lin_dspring_rot
(opt_material, material, virtual, state)- Arguments:
opt_material :
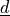
material :
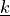
virtual:

state:

Stiffness matrix
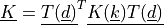 is defined by 6 components
is defined by 6 components
![\ul{k} = [k_{u1}, k_{u2}, k_{u3}, k_{r1}, k_{r2}, k_{r3}]](../../../_images/math/a1f7d6493ac984e9bca27bf5c3b7cc571df0444e.png) in 3D
and by 3 components
in 3D
and by 3 components ![\ul{k} = [k_{u1}, k_{u2}, k_{r1}]](../../../_images/math/7928e48b73c94fec5efc7ce84c26d2e36ed9d04f.png) ,
where
,
where 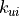 is the stiffness for the displacement DOF
and
is the stiffness for the displacement DOF
and 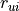 is for the rotational DOF. Note that the components of
is for the rotational DOF. Note that the components of
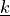 are in the local coordinates system specified by a given
direction
are in the local coordinates system specified by a given
direction 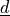 or by the vector
or by the vector
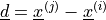 for non-coincidental end nodes.
The stiffness parameter
for non-coincidental end nodes.
The stiffness parameter 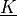 can also be defined as a 6x6 matrix
in 3D or a 3x3 matrix in 2D.
can also be defined as a 6x6 matrix
in 3D or a 3x3 matrix in 2D.- arg_shapes = [{'material': 'S, 1', 'opt_material': 'D, 1', 'state': 'S', 'virtual': ('S', 'state')}, {'material': 'S, S'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'material', 'virtual', 'state')¶
- name = 'dw_lin_dspring_rot'¶
- class sfepy.terms.terms_elastic.LinearDSpringTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear spring element with the stiffness transformed into the element direction.
- Definition:
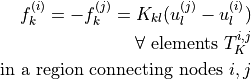
- Call signature:
dw_lin_dspring
(opt_material, material, virtual, state)- Arguments:
opt_material :
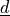
material :
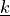
virtual:

state:

Stiffness matrix
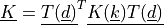 is defined by 6 components
is defined by 6 components
![\ul{k} = [k_{u1}, k_{u2}, k_{u3}, k_{r1}, k_{r2}, k_{r3}]](../../../_images/math/a1f7d6493ac984e9bca27bf5c3b7cc571df0444e.png) in 3D
and by 3 components
in 3D
and by 3 components ![\ul{k} = [k_{u1}, k_{u2}, k_{r1}]](../../../_images/math/7928e48b73c94fec5efc7ce84c26d2e36ed9d04f.png) ,
where
,
where 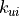 is the stiffness for the displacement DOF
and
is the stiffness for the displacement DOF
and 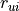 is for the rotational DOF. Note that the components of
is for the rotational DOF. Note that the components of
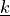 are in the local coordinates system specified by a given
direction
are in the local coordinates system specified by a given
direction 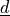 or by the vector
or by the vector
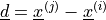 for non-coincidental end nodes.
The stiffness parameter
for non-coincidental end nodes.
The stiffness parameter 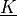 can also be defined as a 6x6 matrix
in 3D or a 3x3 matrix in 2D.
can also be defined as a 6x6 matrix
in 3D or a 3x3 matrix in 2D.- arg_shapes = [{'material': 'D, 1', 'opt_material': 'D, 1', 'state': 'D', 'virtual': ('D', 'state')}, {'material': 'D, D'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'material', 'virtual', 'state')¶
- geometries = ['1_2', '2_1_2', '3_1_2']¶
- integration_order = 0¶
- name = 'dw_lin_dspring'¶
- class sfepy.terms.terms_elastic.LinearElasticETHTerm(name, arg_str, integral, region, **kwargs)[source]¶
This term has the same definition as dw_lin_elastic_th, but assumes an exponential approximation of the convolution kernel resulting in much higher efficiency. Can use derivatives.
- Definition:
![\int_{\Omega} \left [\int_0^t
\Hcal_{ijkl}(t-\tau)\,e_{kl}(\ul{u}(\tau)) \difd{\tau}
\right]\,e_{ij}(\ul{v})](../../../_images/math/e8480ee3ec2210daf9504fe05bc9e759bfd97e14.png)
- Call signature:
dw_lin_elastic_eth
(ts, material_0, material_1, virtual, state)- Arguments:
ts :
TimeStepperinstancematerial_0 :
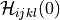
material_1 :
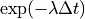 (decay at
(decay at 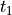 )
)virtual :

state :

- arg_shapes = {'material_0': 'S, S', 'material_1': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('ts', 'material_0', 'material_1', 'virtual', 'state')¶
- static function(out, coef, strain, mtx_d, cmap, is_diff)¶
- get_fargs(ts, mat0, mat1, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_lin_elastic_eth'¶
- class sfepy.terms.terms_elastic.LinearElasticIsotropicTerm(name, arg_str, integral, region, **kwargs)[source]¶
Isotropic linear elasticity term.
- Definition:
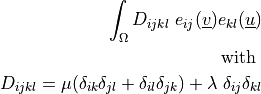
- Call signature:
dw_lin_elastic_iso
(material_1, material_2, virtual, state)(material_1, material_2, parameter_1, parameter_2)- Arguments:
material_1:
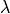
material_2:
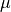
virtual/parameter_1:

state/parameter_2:

- arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material_1', 'material_2', 'virtual', 'state'), ('material_1', 'material_2', 'parameter_1', 'parameter_2'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- get_eval_shape(mat1, mat2, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_lin_elastic_iso'¶
- class sfepy.terms.terms_elastic.LinearElasticTHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Fading memory linear elastic (viscous) term. Can use derivatives.
- Definition:
![\int_{\Omega} \left [\int_0^t
\Hcal_{ijkl}(t-\tau)\,e_{kl}(\ul{u}(\tau)) \difd{\tau}
\right]\,e_{ij}(\ul{v})](../../../_images/math/e8480ee3ec2210daf9504fe05bc9e759bfd97e14.png)
- Call signature:
dw_lin_elastic_th
(ts, material, virtual, state)- Arguments:
ts :
TimeStepperinstancematerial :
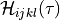
virtual :

state :

- arg_shapes = {'material': '.: N, S, S', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('ts', 'material', 'virtual', 'state')¶
- static function(out, coef, strain, mtx_d, cmap, is_diff)¶
- name = 'dw_lin_elastic_th'¶
- class sfepy.terms.terms_elastic.LinearElasticTerm(name, arg_str, integral, region, **kwargs)[source]¶
General linear elasticity term, with
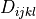 given in
the usual matrix form exploiting symmetry: in 3D it is
given in
the usual matrix form exploiting symmetry: in 3D it is 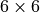 with the indices ordered as
with the indices ordered as ![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in 2D it is
, in 2D it is
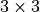 with the indices ordered as
with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) . Can be
evaluated. Can use derivatives.
. Can be
evaluated. Can use derivatives.- Definition:
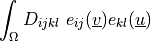
- Call signature:
dw_lin_elastic
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments 1:
material :
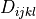
virtual :

state :

- Arguments 2:
material :
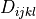
parameter_1 :
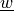
parameter_2 :

- arg_shapes = {'material': 'S, S', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'dw_lin_elastic'¶
- class sfepy.terms.terms_elastic.LinearPrestressTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear prestress term, with the prestress
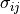 given either
in the usual vector form exploiting symmetry: in 3D it has 6 components
with the indices ordered as
given either
in the usual vector form exploiting symmetry: in 3D it has 6 components
with the indices ordered as ![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in 2D it has
3 components with the indices ordered as
, in 2D it has
3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) , or in the
matrix (possibly non-symmetric) form. Can be evaluated.
, or in the
matrix (possibly non-symmetric) form. Can be evaluated.- Definition:
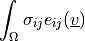
- Call signature:
dw_lin_prestress
(material, virtual)(material, parameter)- Arguments 1:
material :
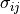
virtual :

- Arguments 2:
material :
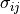
parameter :

- arg_shapes = [{'material': 'S, 1', 'parameter': 'D', 'virtual': ('D', None)}, {'material': 'D, D'}]¶
- arg_types = (('material', 'virtual'), ('material', 'parameter'))¶
- modes = ('weak', 'eval')¶
- name = 'dw_lin_prestress'¶
- class sfepy.terms.terms_elastic.LinearSpringTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear spring element.
- Definition:
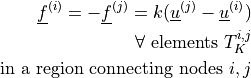
- Call signature:
dw_lin_spring
(material, virtual, state)- Arguments 1:
material :
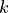
virtual :

state :

- arg_shapes = {'material': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- geometries = ['1_2', '2_1_2', '3_1_2']¶
- integration_order = 0¶
- name = 'dw_lin_spring'¶
- class sfepy.terms.terms_elastic.LinearStrainFiberTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear (pre)strain fiber term with the unit direction vector
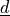 .
.- Definition:
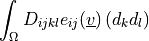
- Call signature:
dw_lin_strain_fib
(material_1, material_2, virtual)- Arguments:
material_1 :
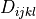
material_2 :
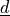
virtual :

- arg_shapes = {'material_1': 'S, S', 'material_2': 'D, 1', 'virtual': ('D', None)}¶
- arg_types = ('material_1', 'material_2', 'virtual')¶
- static function(out, mtx_d, mat, cmap)¶
- name = 'dw_lin_strain_fib'¶
- class sfepy.terms.terms_elastic.LinearTrussInternalForceTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate internal force in the element direction. To be used with ‘el_avg’ or ‘qp’ evaluation modes which give the same results. The material parameter
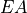 is equal to
Young modulus times element coss-section. The internal force
is given by
is equal to
Young modulus times element coss-section. The internal force
is given by 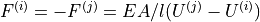 ,
where
,
where 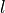 is the element length and
is the element length and 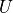 ,
, 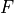 are
the nodal displacements and the nodal forces in the element direction.
are
the nodal displacements and the nodal forces in the element direction.- Definition:
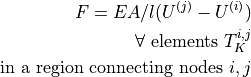
- Call signature:
ev_lin_truss_force
(material, parameter)- Arguments:
material :
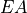
parameter :
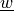
- arg_shapes = {'material': '1, 1', 'parameter': 'D'}¶
- arg_types = ('material', 'parameter')¶
- geometries = ['1_2', '2_1_2', '3_1_2']¶
- integration_order = 0¶
- name = 'ev_lin_truss_force'¶
- class sfepy.terms.terms_elastic.LinearTrussTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate internal force in the element direction. To be used with ‘el_avg’ or ‘qp’ evaluation modes which give the same results. The material parameter
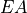 is equal to
Young modulus times element coss-section. The internal force
is given by
is equal to
Young modulus times element coss-section. The internal force
is given by 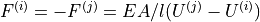 ,
where
,
where 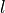 is the element length and
is the element length and 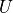 ,
, 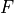 are
the nodal displacements and the nodal forces in the element direction.
are
the nodal displacements and the nodal forces in the element direction.- Definition:
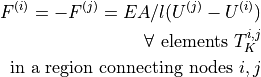
- Call signature:
dw_lin_truss
(material, virtual, state)- Arguments:
material :
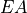
parameter :
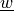
- arg_shapes = {'material': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- geometries = ['1_2', '2_1_2', '3_1_2']¶
- integration_order = 0¶
- name = 'dw_lin_truss'¶
- class sfepy.terms.terms_elastic.NonsymElasticTerm(name, arg_str, integral, region, **kwargs)[source]¶
Elasticity term with non-symmetric gradient. The indices of matrix
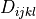 are ordered as
are ordered as
![[11, 12, 13, 21, 22, 23, 31, 32, 33]](../../../_images/math/c7c8170f591e15d2d2117b1e0e7890de0ccb51c9.png) in 3D and as
in 3D and as
![[11, 12, 21, 22]](../../../_images/math/d09e36805a25ebb6c9fbe034ff6223d83d852d5e.png) in 2D.
in 2D.- Definition:
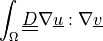
- Call signature:
dw_nonsym_elastic
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments 1:
material :
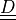
virtual :

state :

- Arguments 2:
material :
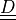
parameter_1 :
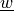
parameter_2 :

- arg_shapes = {'material': 'D2, D2', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- modes = ('weak', 'eval')¶
- name = 'dw_nonsym_elastic'¶
- class sfepy.terms.terms_elastic.SDLinearElasticTerm(name, arg_str, integral, region, **kwargs)[source]¶
Sensitivity analysis of the linear elastic term.
- Definition:
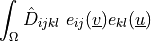
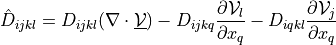
- Call signature:
ev_sd_lin_elastic
(material, parameter_w, parameter_u, parameter_mv)- Arguments:
material :
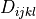
parameter_w :
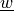
parameter_u :

parameter_mv :
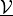
- arg_shapes = {'material': 'S, S', 'parameter_mv': 'D', 'parameter_u': 'D', 'parameter_w': 'D'}¶
- arg_types = ('material', 'parameter_w', 'parameter_u', 'parameter_mv')¶
- static function(out, coef, grad_v, grad_u, grad_w, mtx_d, cmap)¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- get_eval_shape(mat, par_w, par_u, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'ev_sd_lin_elastic'¶