sfepy.terms.terms_shells module¶
Terms implementing shell elements.
- class sfepy.terms.terms_shells.Shell10XTerm(name, arg_str, integral, region, **kwargs)[source]¶
The shell10x element term based on the Reissner-Mindlin theory [1], [2], corresponding to a shell of thickness
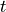 .
.The term requires a custom 3D quadrature, where the
 components of
quadrature point coordinates are transformed from
components of
quadrature point coordinates are transformed from ![[0, 1]](../../../_images/math/f230f99d598bee0a0cd2ccbc3cdc7d607ac2056b.png) to
to
![[-t/2, t/2]](../../../_images/math/a83d2c5aa4ae12024bc7ebb039473e46c62115c1.png) , and the quadrature weights are multiplied by
, and the quadrature weights are multiplied by
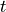 . The variables
. The variables  and
and  have to use
have to use
Shell10XFieldand have six components. The reference element mapping is implemented byShell10XMapping. The term does not implement the piezo-electric components of the shell10x element yet.The term has to be used with quadrilateral cells in 3D and should behave as the linear elastic term, but with fewer degrees of freedom for the same accuracy for shell-like structures. The shell has six degrees of freedom in each of the four nodes:
![{\mathbf u}_i = [ u_i, v_i, w_i, \alpha_i,
\beta_i, \gamma_i ]^T](../../../_images/math/3359e2f7f63f1890bdccea68df145ea29a5a55ad.png) ,
, 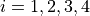 . The strain and stress
vectors are calculated in a local (co-rotational) coordinate system given
by basis vectors
. The strain and stress
vectors are calculated in a local (co-rotational) coordinate system given
by basis vectors 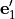 ,
, 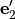 and
and
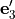 . It holds that
. It holds that![[ u'_i, v'_i, w'_i, \alpha'_i, \beta'_i, \gamma'_i ]^T
= {\hat{\mathbf H}}^T{\mathbf u}_i\,](../../../_images/math/72f11869ad77aded25cb31e5771bb649201ef36b.png)
where
![{\hat{\mathbf H}} = \left[ \begin{array}{cc} {\mathbf H} & \\ & {\mathbf
H} \\ \end{array} \right]\qquad
{\mathrm{and}} \qquad {\mathbf H} =
[{\mathbf e}'_1 \, {\mathbf e}'_2 \, {\mathbf e}'_3]](../../../_images/math/9980dabdb0b5ffc8b7a308590999d79e4a87b3d2.png)
is a nodal DOF transformation matrix.
The local displacements
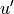 ,
, 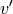 and
and 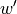 at any point
in the layer characterized by the isoparametric coordinates
at any point
in the layer characterized by the isoparametric coordinates 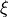 ,
,
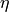 and
and 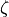 (
(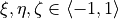 ) are interpolated from the nodal
displacement and rotation values (i.e. both membrane and bending
components) using standard isoparametric approximation functions for a
quadrilateral, hence
) are interpolated from the nodal
displacement and rotation values (i.e. both membrane and bending
components) using standard isoparametric approximation functions for a
quadrilateral, hence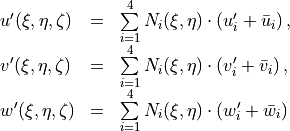
where
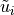 ,
, 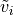 and
and 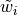 are
the bending components of displacements calculated from displacements due
to rotations
are
the bending components of displacements calculated from displacements due
to rotations 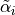 and
and 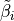 about
local nodal axes
about
local nodal axes 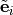 as
as![\left[ \begin{array}{c} \bar{u}\\ \bar{v}\\ \bar{w}\\ \end{array}
\right]_i = \tilde{\zeta} \left[ \begin{array}{cc} & \\
\tilde{\mathbf{e}}_1 & -\tilde{\mathbf{e}}_2 \\ & \\ \end{array}
\right]_i \left[ \begin{array}{c}
\tilde{\mathbf{e}}_2^T \\ \tilde{\mathbf{e}}_1^T \\ \end{array}
\right]_i \left[ \begin{array}{c} \alpha' \\ \beta' \\ \gamma' \\
\end{array} \right]_i \,](../../../_images/math/bb9f1635dba5088babafe7547d5ba333386b1291.png)
where
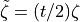 . The local nodal axes
. The local nodal axes
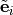 are constructed in order to describe the
behavior of warped (non-planar) elements adequately.
are constructed in order to describe the
behavior of warped (non-planar) elements adequately.The term employs three shell element enhancements:
DSG method
EAS method
drilling rotations lock (parameter
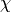 - a good value is about
- a good value is about
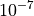 )
)
For detailed theoretical information see the references.
[1]Zemčík, R., Rolfes, R., Rose, M. and Tessmer, J. (2006),
High-Performance 4-Node Shell Element with Piezoelectric Coupling Mechanics of Advanced Materials and Structures Vol. 13, Iss. 5, doi:10.1080/15376490600777657
[2]Zemčík, R., Rolfes, R., Rose, M. and Teßmer, J. (2007),
High-performance four-node shell element with piezoelectric coupling for the analysis of smart laminated structures. Int. J. Numer. Meth. Engng., 70: 934–961. doi:10.1002/nme.1909
- Definition:
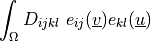
- Call signature:
dw_shell10x
(material_d, material_drill, virtual, state)- Arguments:
material_d :
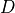
material_drill :
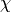
virtual :

state :

- arg_shapes = {'material_d': '6, 6', 'material_drill': '.: 1', 'state': 6, 'virtual': (6, 'state')}¶
- arg_types = ('material_d', 'material_drill', 'virtual', 'state')¶
- geometries = ['3_2_4']¶
- get_fargs(mtx_d, drill, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_physical_qps()[source]¶
Get physical quadrature points corresponding to the term region and integral.
- integration = 'custom'¶
- name = 'dw_shell10x'¶
- poly_space_basis = 'shell10x'¶