sfepy.linalg.eigen module¶

sfepy.linalg.eigen.cg_eigs(mtx, rhs=None, precond=None, i_max=None, eps_r=1e-10, shift=None, select_indices=None, verbose=False, report_step=10)[source]¶

Make several iterations of the conjugate gradients and estimate so the eigenvalues of a (sparse SPD) matrix (Lanczos algorithm).

Parameters:

mtxspmatrix or array: The sparse matrix $A$ .
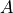precondspmatrix or array, optional: The preconditioner matrix. Any object that can be multiplied by vector can be passed.
i_maxint: The maximum number of the Lanczos algorithm iterations.
eps_rfloat: The relative stopping tolerance.
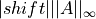shiftfloat, optional: Eigenvalue shift for non-SPD matrices. If negative, the shift is computed as $|shift| ||A||_{\infty}$ .
select_indices(min, max), optional: If given, computed only the eigenvalues with indices min <= i <= max.
verbosebool: Verbosity control.
report_stepint: If verbose is True, report in every report_step-th step.

Returns:

vecarray: The approximate solution to the linear system.
n_itint: The number of CG iterations used.
norm_rsarray: Convergence history of residual norms.
eigsarray: The approximate eigenvalues sorted in ascending order.

sfepy.linalg.eigen.sym_tri_eigen(diags, select_indices=None)[source]¶: Compute eigenvalues of a symmetric tridiagonal matrix using scipy.linalg.eigvals_banded().