sfepy.homogenization.recovery module¶

sfepy.homogenization.recovery.add_strain_rs(corrs_rs, strain, vu, dim, iel, out=None)[source]¶

sfepy.homogenization.recovery.add_stress_p(out, pb, integral, region, vp, data)[source]¶

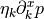
sfepy.homogenization.recovery.combine_scalar_grad(corrs, grad, vn, ii, shift_coors=None)[source]¶: $\eta_k \partial_k^x p$

or

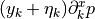
$(y_k + \eta_k) \partial_k^x p$

sfepy.homogenization.recovery.compute_mac_stress_part(pb, integral, region, material, vu, mac_strain)[source]¶

sfepy.homogenization.recovery.compute_micro_u(corrs, strain, vu, dim, out=None)[source]¶: Micro displacements.

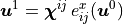
$\bm{u}^1 = \bm{\chi}^{ij}\, e_{ij}^x(\bm{u}^0)$

sfepy.homogenization.recovery.compute_p_corr_steady(corrs_pressure, pressure, vp, iel)[source]¶: $\widetilde\pi^P\,p$

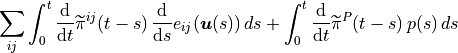
sfepy.homogenization.recovery.compute_p_corr_time(corrs_rs, dstrains, corrs_pressure, pressures, vdp, dim, iel, ts)[source]¶: $\sum_{ij} \int_0^t {\mathrm{d} \over \mathrm{d} t} \widetilde\pi^{ij}(t-s)\, {\mathrm{d} \over \mathrm{d} s} e_{ij}(\bm{u}(s))\,ds + \int_0^t {\mathrm{d} \over \mathrm{d} t}\widetilde\pi^P(t-s)\,p(s)\,ds$

sfepy.homogenization.recovery.compute_p_from_macro(p_grad, coor, iel, centre=None, extdim=0)[source]¶: Macro-induced pressure.

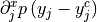
$\partial_j^x p\,(y_j - y_j^c)$

sfepy.homogenization.recovery.compute_stress_strain_u(pb, integral, region, material, vu, data)[source]¶

sfepy.homogenization.recovery.compute_u_corr_steady(corrs_rs, strain, vu, dim, iel)[source]¶

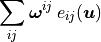
$\sum_{ij} \bm{\omega}^{ij}\, e_{ij}(\bm{u})$

Notes

iel = element number

sfepy.homogenization.recovery.compute_u_corr_time(corrs_rs, dstrains, corrs_pressure, pressures, vu, dim, iel, ts)[source]¶: $\sum_{ij} \left[ \int_0^t \bm{\omega}^{ij}(t-s) {\mathrm{d} \over \mathrm{d} s} e_{ij}(\bm{u}(s))\,ds\right] + \int_0^t \widetilde{\bm{\omega}}^P(t-s)\,p(s)\,ds$

sfepy.homogenization.recovery.compute_u_from_macro(strain, coor, iel, centre=None)[source]¶: Macro-induced displacements.

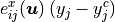
$e_{ij}^x(\bm{u})\,(y_j - y_j^c)$

sfepy.homogenization.recovery.convolve_field_scalar(fvars, pvars, iel, ts)[source]¶

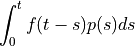
$\int_0^t f(t-s) p(s) ds$

Notes

t is given by step
f: fvars scalar field variables, defined in a micro domain, have shape [step][fmf dims]
p: pvars scalar point variables, a scalar in a point of macro-domain, FMField style have shape [n_step][var dims]

sfepy.homogenization.recovery.convolve_field_sym_tensor(fvars, pvars, var_name, dim, iel, ts)[source]¶

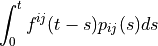
$\int_0^t f^{ij}(t-s) p_{ij}(s) ds$

Notes

t is given by step
f: fvars field variables, defined in a micro domain, have shape [step][fmf dims]
p: pvars sym. tensor point variables, a scalar in a point of macro-domain, FMField style, have shape [dim, dim][var_name][n_step][var dims]

sfepy.homogenization.recovery.destroy_pool()[source]¶

sfepy.homogenization.recovery.get_output_suffix(iel, ts, naming_scheme, format, output_format)[source]¶

sfepy.homogenization.recovery.get_recovery_points(region, eps0)[source]¶

sfepy.homogenization.recovery.recover_bones(problem, micro_problem, region, eps0, ts, strain, dstrains, p_grad, pressures, corrs_permeability, corrs_rs, corrs_time_rs, corrs_pressure, corrs_time_pressure, var_names, naming_scheme='step_iel')[source]¶

Notes

note that

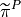
$\widetilde{\pi}^P$

is in corrs_pressure -> from time correctors only ‘u’, ‘dp’ are needed.

sfepy.homogenization.recovery.recover_micro_hook(micro_filename, region, macro, eps0, region_mode='el_centers', eval_mode='constant', eval_vars=None, corrs=None, recovery_file_tag='', define_args=None, output_dir=None, verbose=False)[source]¶

Parameters:

micro_filenamestr: The definition file of the microproblem.
regionRegion or array: The macroscopic region to be recovered. If array, the centers of microscopic RVEs (Representative Volume Element) are assumed to be stored in it. If Region, the RVE centers are computed according to region_mode, see below.
macrodict of arrays or tuples: Either macroscopic values (if array) or the tuple (mode, eval_var, nodal_values) is expected. The tuple is used to evaluate the macroscopic values in given points of RVEs (see ‘eval_mode`). mode can be ‘val’, ‘grad’, ‘div’, or ‘cauchy_strain’.
eps0float: The size of the microstructures (RVE).
region_mode{‘el_centers’, ‘tiled’}: If ‘el_centers’, the RVE centers are identical to the element centers of the macroscopic FE mesh. If ‘tiled’, the recovered region is tiled by rescaled RVEs.
eval_mode{‘constant’, ‘continuous’}: If ‘constant’, the macroscopic fields are evaluated only at the RVE centers. If ‘continuous’, the fields are evaluated at all points of the RVE mesh.
eval_varslist of variables: The list of variables use to evaluate the macroscopic fields.
corrsdict of CorrSolution: The correctors for recovery.
recovery_file_tagstr: The tag which is appended to the output file.
define_argsdict: The define arguments for the microscopic problem.
output_dirstr: The output directory.
verbosebool: The verbose terminal output.

sfepy.homogenization.recovery.recover_paraflow(problem, micro_problem, region, ts, strain, dstrains, pressures1, pressures2, corrs_rs, corrs_time_rs, corrs_alpha1, corrs_time_alpha1, corrs_alpha2, corrs_time_alpha2, var_names, naming_scheme='step_iel')[source]¶

sfepy.homogenization.recovery.save_recovery_region(mac_pb, rname, filename=None)[source]¶