sfepy.homogenization.convolutions module¶
- class sfepy.homogenization.convolutions.ConvolutionKernel(name, times, kernel, decay=None, exp_coefs=None, exp_decay=None)[source]¶
The convolution kernel with exponential synchronous decay approximation approximating the original kernel represented by the array
![c[i]](../../../_images/math/0980ecc5d8385810149c3a5f41f595c156137ba8.png) ,
,
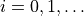 .
.![\begin{split}
& c_0 \equiv c[0] \;, c_{e0} \equiv c_0 c^e_0 \;, \\
& c(t) \approx c_0 d(t) \approx c_0 e(t) = c_{e0} e_n(t) \;,
\end{split}](../../../_images/math/81ac324781faf75f727150401fc4150d788a9a87.png)
where
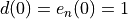 ,
, 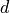 is the synchronous decay and
is the synchronous decay and
 its
exponential approximation,
its
exponential approximation, 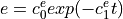 .
.
- sfepy.homogenization.convolutions.approximate_exponential(x, y)[source]¶
Approximate
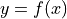 by
by 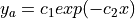 .
.Initial guess is given by assuming y has already the required exponential form.
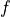 by an exponential.
by an exponential.