linear_elasticity/two_bodies_contact.py¶
Description
Contact of two elastic bodies with a penalty function for enforcing the contact constraints.
Find 
such that:
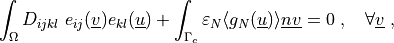
where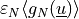 
is the penalty
function,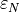 
is the normal penalty parameter, 
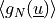are the Macaulay’s brackets of the gap function
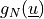and
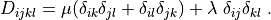
This example also demonstrates use of an experimental contact term based on the IPC Toolkit [1].
[1] https://github.com/ipc-sim/ipc-toolkit
Usage examples:
# Check regions and EBC nodes.
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py --save-regions-as-groups --save-ebc-nodes --solve-not
sfepy-view two_bodies_ebc_nodes.vtk
sfepy-view two_bodies_regions.h5
# Run with default parameters and view results.
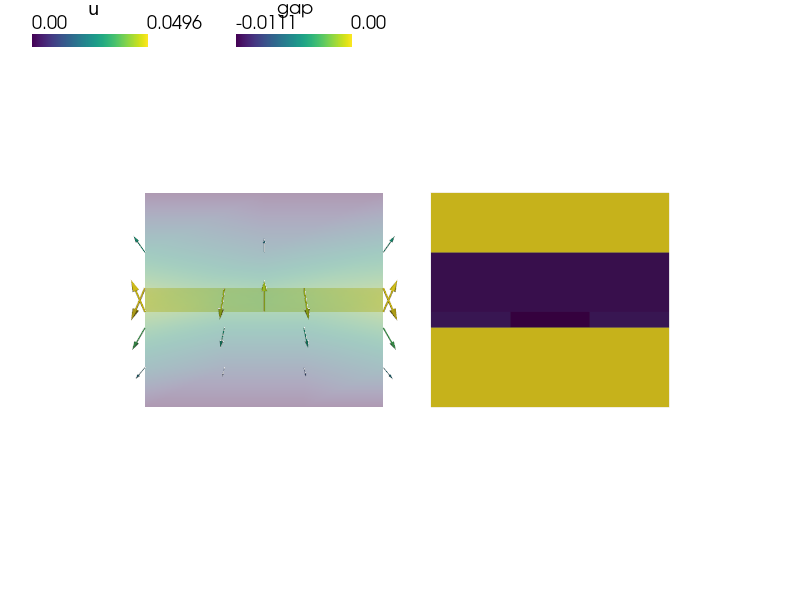
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py
sfepy-view output/contact/two_bodies.h5
sfepy-view output/contact/two_bodies.h5 -f u:wu:f1:p0 1:vw:wu:f1:p0
# Plot the nonlinear solver convergence.
python3 sfepy/scripts/plot_logs.py output/contact/log.txt
# Run with default parameters and IPC toolkit, view results.
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py -d "contact='ipc'"
sfepy-view output/contact/two_bodies.h5 -f u:wu:f1:p0 1:vw:wu:f1:p0
# Plot the IPC contact parameters evolution.
python3 sfepy/scripts/plot_logs.py output/contact/clog.txt
r"""
Contact of two elastic bodies with a penalty function for enforcing the contact
constraints.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
+ \int_{\Gamma_{c}} \varepsilon_N \langle g_N(\ul{u}) \rangle \ul{n} \ul{v}
= 0
\;, \quad \forall \ul{v} \;,
where :math:`\varepsilon_N \langle g_N(\ul{u}) \rangle` is the penalty
function, :math:`\varepsilon_N` is the normal penalty parameter, :math:`\langle
g_N(\ul{u}) \rangle` are the Macaulay's brackets of the gap function
:math:`g_N(\ul{u})` and
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
This example also demonstrates use of an experimental contact term based on the
IPC Toolkit [1].
[1] https://github.com/ipc-sim/ipc-toolkit
Usage examples::
# Check regions and EBC nodes.
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py --save-regions-as-groups --save-ebc-nodes --solve-not
sfepy-view two_bodies_ebc_nodes.vtk
sfepy-view two_bodies_regions.h5
# Run with default parameters and view results.
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py
sfepy-view output/contact/two_bodies.h5
sfepy-view output/contact/two_bodies.h5 -f u:wu:f1:p0 1:vw:wu:f1:p0
# Plot the nonlinear solver convergence.
python3 sfepy/scripts/plot_logs.py output/contact/log.txt
# Run with default parameters and IPC toolkit, view results.
sfepy-run sfepy/examples/linear_elasticity/two_bodies_contact.py -d "contact='ipc'"
sfepy-view output/contact/two_bodies.h5 -f u:wu:f1:p0 1:vw:wu:f1:p0
# Plot the IPC contact parameters evolution.
python3 sfepy/scripts/plot_logs.py output/contact/clog.txt
"""
import os.path as op
from functools import partial
import inspect
from sfepy.base.base import output
from sfepy.base.log import Log
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.discrete.fem.meshio import UserMeshIO
import numpy as nm
def get_bbox(dims, centre, eps=0.0):
dims = nm.asarray(dims)
centre = nm.asarray(centre)
bbox = nm.r_[[centre - (0.5 - eps) * dims], [centre + (0.5 - eps) * dims]]
return bbox
def gen_two_bodies(dims0, shape0, centre0, dims1, shape1, centre1, shift1):
from sfepy.discrete.fem import Mesh
from sfepy.mesh.mesh_generators import gen_block_mesh
m0 = gen_block_mesh(dims0, shape0, centre0)
m1 = gen_block_mesh(dims1, shape1, centre1)
coors = nm.concatenate((m0.coors, m1.coors + shift1), axis=0)
desc = m0.descs[0]
c0 = m0.get_conn(desc)
c1 = m1.get_conn(desc)
conn = nm.concatenate((c0, c1 + m0.n_nod), axis=0)
ngroups = nm.zeros(coors.shape[0], dtype=nm.int32)
ngroups[m0.n_nod:] = 1
mat_id = nm.zeros(conn.shape[0], dtype=nm.int32)
mat_id[m0.n_el:] = 1
name = 'two_bodies'
mesh = Mesh.from_data(name, coors, ngroups, [conn], [mat_id], m0.descs)
return mesh
def find_contact_ipc_term(equations):
for eq in equations:
for term in eq.terms:
if term.name == 'dw_contact_ipc':
break
else:
continue
break
else:
raise ValueError('no dw_contact_ipc in equations!')
return term
def apply_line_search(vec_x0, vec_dx0, it, err_last, conf, fun,
timers, log=None, context=None, clog=None):
"""
Apply a backtracking line-search with continuous collision detection from
IPC toolkit.
"""
pb = context
term = find_contact_ipc_term(pb.equations)
select_other = lambda term: term.name != 'dw_contact_ipc'
ls = 1.0
vec_dx = vec_dx0
variables = pb.get_variables()
ci = term.get_contact_info(variables['u'])
ci.it = it
ls_it = 0
while 1:
vec_x = vec_x0 - vec_dx
if it > 0:
# Determine max. step size using continuous collision detection.
u0 = variables.make_full_vec(vec_x0).reshape((-1, ci.dim))
u1 = variables.make_full_vec(vec_x).reshape((-1, ci.dim))
x0 = ci.smesh.coors + u0[ci.nods]
x1 = ci.smesh.coors + u1[ci.nods]
max_step_size = term.ipc.compute_collision_free_stepsize(
ci.collision_mesh, x0, x1,
)
if max_step_size < 1.0:
vec_x = vec_x0 - max_step_size * vec_dx
ls = min(ls, max_step_size)
timers.residual.start()
ci.ls_it = ls_it
try:
vec_r1 = fun(vec_x, select_term=select_other)
vec_r1_full = pb.equations.make_full_vec(vec_r1, force_value=0.0)
ci.e_grad_full = vec_r1_full
val, iels = term.evaluate(mode='weak', dw_mode='vector',
standalone=False, ci=ci)
vec_r2 = nm.zeros_like(vec_r1)
term.assemble_to(vec_r2, val, iels, mode='vector')
vec_r = vec_r1 + vec_r2
except ValueError:
if (it == 0) or (ls < conf.ls_min):
output('giving up!')
raise
else:
ok = False
else:
ok = True
timers.residual.stop()
if ok:
err = nm.linalg.norm(vec_r)
if not nm.isfinite(err):
output('residual:', vec_r)
output(nm.isfinite(vec_r).all())
raise ValueError('infs or nans in the residual')
if log is not None:
log(err, it)
if clog is not None:
if it > 0:
clog(ci.min_distance, ci.barrier_stiffness,
ci.bp_grad_norm, ci.e_grad_norm)
else:
clog(nm.nan, nm.nan, nm.nan, nm.nan)
if (it == 0) or (err < (err_last * conf.ls_on)):
break
red = conf.ls_red
output('linesearch: iter %d, (%.5e < %.5e) (new ls: %e)'
% (it, err, err_last * conf.ls_on, red * ls))
else: # Failure.
if conf.give_up_warp:
output('giving up!')
break
red = conf.ls_red_warp
output('residual computation failed for iter %d'
' (new ls: %e)!' % (it, red * ls))
if ls < conf.ls_min:
output('linesearch failed, continuing anyway')
break
ls *= red
vec_dx = ls * vec_dx0
ls_it += 1
return vec_x, vec_r, err, ok
def markdown_table_from_dict(adict):
header = '| option | value |\n'
separator = '| --- | --- |\n'
rows = '\n'.join([f'| {key} | {val} |' for key, val in adict.items()])
return header + separator + rows
def define(
dims0=(1.0, 1.0, 0.5),
shape0=(2, 2, 2),
centre0=(0, 0, -0.25),
dims1=(1.2, 0.8, 0.5),
shape1=(3, 3, 2),
centre1=(0, 0, 0.25),
shift10=(0.0, 0.0, 1e-4),
shift11=(0.0, 0.0, -0.1),
young=1.0,
poisson=0.3,
rho=1.0,
cm=None,
ck=0.0,
dhat=1e-2,
pspd='NONE',
t1=1000,
n_step=5,
contact='builtin',
output_dir='output/contact',
verbose=True,
):
args = locals()
inodir = partial(op.join, output_dir)
output.set_output(filename=inodir('output_log.txt'), quiet=not verbose,
combined=True)
signature = inspect.signature(define)
arg_names = list(signature.parameters.keys())
options = {name : args[name] for name in arg_names}
table = markdown_table_from_dict(options)
with open(inodir('options.md'), 'w') as fd:
fd.write(table)
dim = len(dims0)
shape0 = shape0[:dim]
centre0 = centre0[:dim]
dims1 = dims1[:dim]
shape1 = shape1[:dim]
centre1 = centre1[:dim]
shift10 = shift10[:dim]
shift11 = shift11[:dim]
shift11 = nm.array(shift11)
clog = Log([[r'$d$'], [r'$k$'], [r'$\nabla B$'], [r'$\nabla E$']],
xlabels=['', '', 'all iterations', 'all iterations'],
ylabels=[r'$d$', r'$k$', r'$\nabla B$', r'$\nabla E$'],
yscales=['log', 'linear', 'linear', 'linear'],
is_plot=False,
log_filename=inodir('clog.txt'),
formats=[['%.8e']] * 4)
def mesh_hook(mesh, mode):
if mode == 'read':
return gen_two_bodies(dims0, shape0, centre0,
dims1, shape1, centre1, shift10)
elif mode == 'write':
pass
def post_process(out, pb, state, extend=False):
from sfepy.base.base import Struct
from sfepy.discrete.fem import extend_cell_data
ev = pb.evaluate
gap = ev('dw_contact.i.Contact(contact.epss, v, u)',
mode='el_avg', term_mode='gap')
gap = extend_cell_data(gap, pb.domain, 'Contact', val=0.0,
is_surface=True)
out['gap'] = Struct(name='output_data',
mode='cell', data=gap, dofs=None)
return out
filename_mesh = UserMeshIO(mesh_hook)
options = {
'nls' : 'newton',
'ls' : 'ls',
'output_dir' : output_dir,
'output_format' : 'h5',
'post_process_hook' : 'post_process',
}
bbox0 = get_bbox(dims0, centre0, eps=1e-5)
bbox1 = get_bbox(dims1, nm.asarray(centre1) + nm.asarray(shift10), eps=1e-5)
if dim == 2:
regions = {
'Omega' : 'all',
'Omega0' : 'cells of group 0',
'Omega1' : 'cells of group 1',
'Bottom' : ('vertices in (y < %.12e)' % bbox0[0, 1], 'facet'),
'Top' : ('vertices in (y > %.12e)' % bbox1[1, 1], 'facet'),
'Contact0' : ('(vertices in (y > %.12e) *v r.Omega0)' % bbox0[1, 1],
'facet'),
'Contact1' : ('(vertices in (y < %.12e) *v r.Omega1)' % bbox1[0, 1],
'facet'),
'Contact' : ('r.Contact0 +s r.Contact1', 'facet')
}
else:
regions = {
'Omega' : 'all',
'Omega0' : 'cells of group 0',
'Omega1' : 'cells of group 1',
'Bottom' : ('vertices in (z < %.12e)' % bbox0[0, 2], 'facet'),
'Top' : ('vertices in (z > %.12e)' % bbox1[1, 2], 'facet'),
'Contact0' : ('(vertices in (z > %.12e) *v r.Omega0)' % bbox0[1, 2],
'facet'),
'Contact1' : ('(vertices in (z < %.12e) *v r.Omega1)' % bbox1[0, 2],
'facet'),
'Contact' : ('r.Contact0 +s r.Contact1', 'facet')
}
fields = {
'displacement': ('real', dim, 'Omega', 1),
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
}
ebcs = {
'fixb' : ('Bottom', {'u.all' : 0.0}),
'fixt' : ('Top', {'u.all' : 'move_top'}),
}
def move_top(ts, coors, bc, problem, **kwargs):
val = nm.empty_like(coors)
val[:] = ts.nt * shift11
return val
functions = {
'move_top' : (move_top,),
}
volume = nm.prod(dims0) + nm.prod(dims1)
mass = volume * rho
materials = {
'solid' : ({
'D' : stiffness_from_youngpoisson(dim, young=young, poisson=poisson),
},),
'contact' : ({
'.m' : cm if cm is not None else mass,
'.k' : ck, # 0 = Adaptive barrier stiffness.
'.dhat' : dhat,
'.Pspd' : pspd,
'.epss' : 2e+1,
},),
}
integrals = {
'i' : 2,
}
if contact == 'builtin':
equations = {
'elasticity' :
"""
dw_lin_elastic.2.Omega(solid.D, v, u)
+ dw_contact.i.Contact(contact.epss, v, u)
= 0
""",
}
elif contact == 'ipc':
equations = {
'elasticity' :
"""
dw_lin_elastic.2.Omega(solid.D, v, u)
+ dw_contact_ipc.i.Contact(
contact.m, contact.k, contact.dhat, contact.Pspd, v, u
)
= 0
""",
}
else:
raise ValueError("contact argument can be one of 'builtin', 'ipc'!")
if contact == 'ipc':
apply_ls = partial(apply_line_search, clog=clog)
else:
apply_ls = None
solvers = {
'ls' : ('ls.auto_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 30,
'eps_a' : 1e-8,
'eps_r' : 1e-8,
'eps_mode' : 'or',
'macheps' : 1e-16,
# Linear system error < (eps_a * lin_red).
'lin_red' : None,
'line_search_fun' : apply_ls,
'ls_red' : 0.5,
'ls_red_warp' : 0.5,
'ls_on' : 1.0,
'ls_min' : 1e-5,
'check' : 0,
'delta' : 1e-8,
'log' : {'text' : inodir('log.txt')},
'log_vlines' : 'solve',
}),
'ts' : ('ts.simple', {
't0' : 0.0,
't1' : t1,
'dt' : None,
'n_step' : n_step,
'quasistatic' : True,
'verbose' : 1,
}),
}
return locals()