linear_elasticity/linear_viscoelastic.py¶

Description

Linear viscoelasticity with pressure traction load on a surface and constrained to one-dimensional motion.

The fading memory terms require an unloaded initial configuration, so the load starts in the second time step. The load is then held for the first half of the total time interval, and released afterwards.

This example uses exponential fading memory kernel 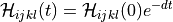$\Hcal_{ijkl}(t) = \Hcal_{ijkl}(0) e^{-d t}$ with decay 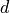$d$ . Two equation kinds are supported - ‘th’ and ‘eth’. In ‘th’ mode the tabulated kernel is linearly interpolated to required times using interp_conv_mat(). In ‘eth’ mode, the computation is exact for exponential kernels.

Find $\ul{u}$ such that:

$\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u}) \\ + \int_{\Omega} \left [\int_0^t \Hcal_{ijkl}(t-\tau)\,e_{kl}(\pdiff{\ul{u}}{\tau}(\tau)) \difd{\tau} \right]\,e_{ij}(\ul{v}) \\ = - \int_{\Gamma_{right}} \ul{v} \cdot \ull{\sigma} \cdot \ul{n} \;, \quad \forall \ul{v} \;,$

where

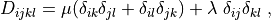
$D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) + \lambda \ \delta_{ij} \delta_{kl} \;,$

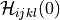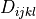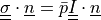$\Hcal_{ijkl}(0)$ has the same structure as $D_{ijkl}$ and $\ull{\sigma} \cdot \ul{n} = \bar{p} \ull{I} \cdot \ul{n}$ with given traction pressure $\bar{p}$ .

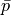Notes¶

Because this example is run also as a test, it uses by default very few time steps. Try changing that.

Visualization¶

The output file is assumed to be ‘block.h5’ in the working directory. Change it appropriately for your situation.

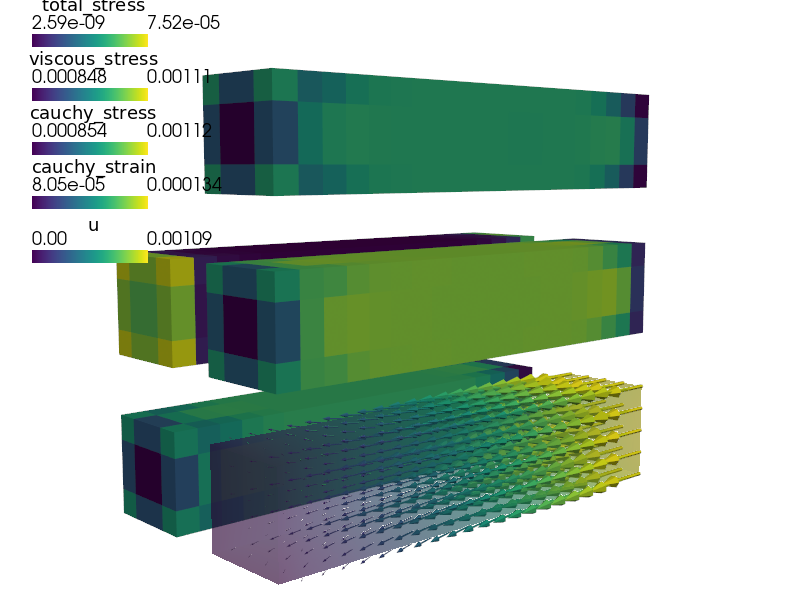
Deforming mesh¶

Try to run the following:

sfepy-view block.h5 -s 20 -f u:wu:f1e0:p0 1:vw:p0 total_stress:p1

to see the results.

Time history plots¶

Run the following:

python3 sfepy/examples/linear_elasticity/linear_viscoelastic.py -h
python3 sfepy/examples/linear_elasticity/linear_viscoelastic.py block.h5

Try comparing ‘th’ and ‘eth’ versions, e.g., for n_step = 201, and f_n_step = 51. There is a visible notch on viscous stress curves in the ‘th’ mode, as the fading memory kernel is cut off before it goes close enough to zero.

../_images/linear_elasticity-linear_viscoelastic1.png

source code

#!/usr/bin/env python
r"""
Linear viscoelasticity with pressure traction load on a surface and constrained
to one-dimensional motion.

The fading memory terms require an unloaded initial configuration, so the load
starts in the second time step. The load is then held for the first half of the
total time interval, and released afterwards.

This example uses exponential fading memory kernel
:math:`\Hcal_{ijkl}(t) = \Hcal_{ijkl}(0) e^{-d t}` with decay
:math:`d`. Two equation kinds are supported - 'th' and 'eth'. In 'th'
mode the tabulated kernel is linearly interpolated to required times
using :func:`interp_conv_mat()`. In 'eth' mode, the computation is exact
for exponential kernels.

Find :math:`\ul{u}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u}) \\
    + \int_{\Omega} \left [\int_0^t
    \Hcal_{ijkl}(t-\tau)\,e_{kl}(\pdiff{\ul{u}}{\tau}(\tau)) \difd{\tau}
    \right]\,e_{ij}(\ul{v}) \\
    = - \int_{\Gamma_{right}} \ul{v} \cdot \ull{\sigma} \cdot \ul{n}
    \;, \quad \forall \ul{v} \;,

where

.. math::
    D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
    \lambda \ \delta_{ij} \delta_{kl}
    \;,

:math:`\Hcal_{ijkl}(0)` has the same structure as :math:`D_{ijkl}` and
:math:`\ull{\sigma} \cdot \ul{n} = \bar{p} \ull{I} \cdot \ul{n}` with
given traction pressure :math:`\bar{p}`.

Notes
-----

Because this example is run also as a test, it uses by default very few time
steps. Try changing that.

Visualization
-------------

The output file is assumed to be 'block.h5' in the working directory. Change it
appropriately for your situation.

Deforming mesh
^^^^^^^^^^^^^^

Try to run the following::

  sfepy-view block.h5 -s 20 -f u:wu:f1e0:p0 1:vw:p0 total_stress:p1

to see the results.

Time history plots
^^^^^^^^^^^^^^^^^^

Run the following::

  python3 sfepy/examples/linear_elasticity/linear_viscoelastic.py -h
  python3 sfepy/examples/linear_elasticity/linear_viscoelastic.py block.h5

Try comparing 'th' and 'eth' versions, e.g., for n_step = 201, and f_n_step =
51. There is a visible notch on viscous stress curves in the 'th' mode, as the
fading memory kernel is cut off before it goes close enough to zero.
"""
import numpy as nm

import sys
sys.path.append('.')

from sfepy.base.base import output
from sfepy.mechanics.matcoefs import stiffness_from_lame
from sfepy.homogenization.utils import interp_conv_mat
from sfepy import data_dir

def linear_tension(ts, coors, mode=None, verbose=True, **kwargs):
    if mode == 'qp':
        val = 1.0 * ((ts.step > 0) and (ts.nt <= 0.5))

        if verbose:
            output('load:', val)

        val = nm.tile(val, (coors.shape[0], 1, 1))

        return {'val' : val}

def get_exp_fading_kernel(coef0, decay, times):
    val = coef0[None, ...] * nm.exp(-decay * times[:, None, None])
    return val

def get_th_pars(ts, coors, mode=None, times=None, kernel=None, **kwargs):
    out = {}

    if mode == 'special':
        out['H'] = interp_conv_mat(kernel, ts, times)

    elif mode == 'qp':
        out['H0'] = kernel[0][None, ...]
        out['Hd'] = nm.array([[[kernel[1, 0, 0] / kernel[0, 0, 0]]]])

    return out

def post_process(out, pb, state, extend=False):
    """
    Calculate and output strain and stress for given displacements.
    """
    from sfepy.base.base import Struct

    ev = pb.evaluate
    strain = ev('ev_cauchy_strain.2.Omega(u)', mode='el_avg')
    out['cauchy_strain'] = Struct(name='output_data', mode='cell',
                                  data=strain, dofs=None)

    estress = ev('ev_cauchy_stress.2.Omega(solid.D, u)', mode='el_avg')
    out['cauchy_stress'] = Struct(name='output_data', mode='cell',
                                  data=estress, dofs=None)

    ts = pb.get_timestepper()
    if pb.conf.mode == 'th':
        vstress = ev('ev_cauchy_stress_th.2.Omega(ts, th.H, du/dt)',
                     ts=ts, mode='el_avg')
        out['viscous_stress'] = Struct(name='output_data', mode='cell',
                                       data=vstress, dofs=None)

    else:
        # The eth terms require 'preserve_caches=True' in order to have correct
        # fading memory history.
        vstress = ev('ev_cauchy_stress_eth.2.Omega(ts, th.H0, th.Hd, du/dt)',
                     ts=ts, mode='el_avg', preserve_caches=True)
        out['viscous_stress'] = Struct(name='output_data', mode='cell',
                                       data=vstress, dofs=None)

    out['total_stress'] = Struct(name='output_data', mode='cell',
                                 data=estress + vstress, dofs=None)

    return out

def define(verbose=False):
    filename_mesh = data_dir + '/meshes/3d/block.mesh'

    ## Configure below. ##

    # Time stepping times.
    t0 = 0.0
    t1 = 20.0
    n_step = 21

    # Fading memory times.
    f_t0 = 0.0
    f_t1 = 5.0
    f_n_step = 6

    decay = 0.8
    mode = 'eth'

    ## Configure above. ##

    times = nm.linspace(f_t0, f_t1, f_n_step)
    kernel = get_exp_fading_kernel(stiffness_from_lame(3, lam=1.0, mu=1.0),
                                   decay, times)

    dt = (t1 - t0) / (n_step - 1)
    fading_memory_length = min(int((f_t1 - f_t0) / dt) + 1, n_step)
    output('fading memory length:', fading_memory_length, verbose=verbose)

    options = {
        'ts' : 'ts',
        'nls' : 'newton',
        'ls' : 'ls',

        'output_format'     : 'h5',
        'post_process_hook' : 'post_process',
    }

    functions = {
        'linear_tension' : (linear_tension,),
        'get_pars' : (lambda ts, coors, mode=None, **kwargs:
                      get_th_pars(ts, coors, mode, times=times, kernel=kernel,
                                  **kwargs),),
    }

    fields = {
        'displacement': ('real', 3, 'Omega', 1),
    }

    materials = {
        'solid' : ({
            'D' : stiffness_from_lame(3, lam=5.769, mu=3.846),
        },),
        'th' : 'get_pars',
        'load' : 'linear_tension',
    }

    variables = {
        'u' : ('unknown field', 'displacement', 0, fading_memory_length),
        'v' : ('test field', 'displacement', 'u'),
    }

    regions = {
        'Omega' : 'all',
        'Left' : ('vertices in (x < -4.99)', 'facet'),
        'Right' : ('vertices in (x > 4.99)', 'facet'),
    }

    ebcs = {
        'fixb' : ('Left', {'u.all' : 0.0}),
        'fixt' : ('Right', {'u.[1,2]' : 0.0}),
    }

    if mode == 'th':
        # General form with tabulated kernel.
        equations = {
            'elasticity' :
            """dw_lin_elastic.2.Omega( solid.D, v, u )
             + dw_lin_elastic_th.2.Omega( ts, th.H, v, du/dt )
             = - dw_surface_ltr.2.Right( load.val, v )""",
        }

    else:
        # Fast form that is exact for exponential kernels.
        equations = {
            'elasticity' :
            """dw_lin_elastic.2.Omega( solid.D, v, u )
             + dw_lin_elastic_eth.2.Omega( ts, th.H0, th.Hd, v, du/dt )
             = - dw_surface_ltr.2.Right( load.val, v )""",
        }

    solvers = {
        'ls' : ('ls.scipy_direct', {}),
        'newton' : ('nls.newton', {
            'i_max' : 1,
            'eps_a' : 1e-10,
        }),
        'ts' : ('ts.simple', {
            't0' : t0,
            't1' : t1,
            'dt' : None,
            'n_step' : n_step,
            'quasistatic' : True,
            'verbose' : 1,
        }),
    }

    return locals()

def main():
    """
    Plot the load, displacement, strain and stresses w.r.t. time.
    """
    from argparse import ArgumentParser, RawDescriptionHelpFormatter
    import matplotlib.pyplot as plt

    from sfepy.base.base import Struct
    import sfepy.postprocess.time_history as th

    msgs = {
        'node': 'plot displacements in given node [default: %(default)s]',
        'element': 'plot tensors in given element [default: %(default)s]',
    }

    parser = ArgumentParser(description=__doc__,
                            formatter_class=RawDescriptionHelpFormatter)
    parser.add_argument(metavar='OUTPUT_FILE', dest='output_file',
                        help='output file in HDF5 format')
    parser.add_argument('-n', '--node', type=int, metavar='ii',
                        action='store', dest='node',
                        default=512, help=msgs['node'])
    parser.add_argument('-e', '--element', type=int, metavar='ii',
                        action='store', dest='element',
                        default=299, help=msgs['element'])
    options = parser.parse_args()

    filename = options.output_file

    tensor_names = ['cauchy_strain',
                    'cauchy_stress', 'viscous_stress', 'total_stress']
    extract = ('u n %d, ' % options.node) \
              + ', '.join('%s e %d' % (name, options.element)
                          for name in tensor_names)
    ths, ts = th.extract_time_history(filename, extract)

    load = [linear_tension(ts, nm.array([0]),
                           mode='qp', verbose=False)['val'].squeeze()
            for ii in ts]
    load = nm.array(load)

    conf = Struct(**define(verbose=True))
    normalized_kernel = conf.kernel[:, 0, 0] / conf.kernel[0, 0, 0]

    plt.figure(1, figsize=(8, 10))
    plt.subplots_adjust(hspace=0.3,
                        top=0.95, bottom=0.05, left=0.07, right=0.95)

    plt.subplot(311)
    plt.plot(conf.times, normalized_kernel, lw=3)
    plt.title('fading memory decay')
    plt.xlabel('time')

    plt.subplot(312)
    plt.plot(ts.times, load, lw=3)
    plt.title('load')
    plt.xlabel('time')

    displacements = ths['u'][options.node]

    plt.subplot(313)
    plt.plot(ts.times, displacements, lw=3)
    plt.title('displacement components, node %d' % options.node)
    plt.xlabel('time')
    plt.tight_layout()

    plt.figure(2, figsize=(8, 10))
    plt.subplots_adjust(hspace=0.35,
                        top=0.95, bottom=0.05, left=0.07, right=0.95)

    for ii, tensor_name in enumerate(tensor_names):
        tensor = ths[tensor_name][options.element]

        plt.subplot(411 + ii)
        plt.plot(ts.times, tensor, lw=3)
        plt.title('%s components, element %d' % (tensor_name, options.element))
        plt.xlabel('time')

    plt.tight_layout()

    plt.show()

if __name__ == '__main__':
    main()