linear_elasticity/its2D_3.py¶
Description
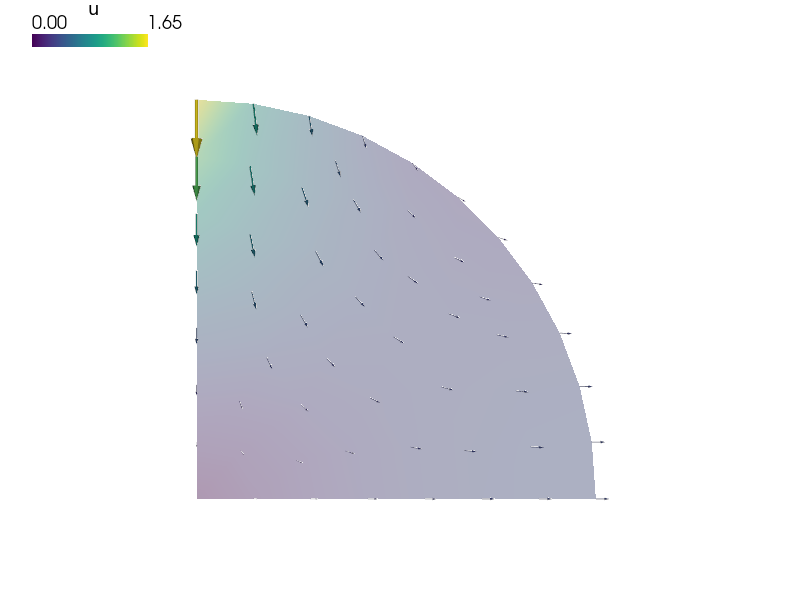
Diametrically point loaded 2-D disk with nodal stress calculation. See Primer.
Find  such that:
such that:
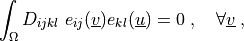
where
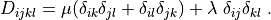
r"""
Diametrically point loaded 2-D disk with nodal stress calculation. See
:ref:`sec-primer`.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
= 0
\;, \quad \forall \ul{v} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
"""
from sfepy.examples.linear_elasticity.its2D_1 import *
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.discrete.fem.geometry_element import geometry_data
from sfepy.discrete import FieldVariable
from sfepy.discrete.fem import Field
import numpy as nm
gdata = geometry_data['2_3']
nc = len(gdata.coors)
def nodal_stress(out, pb, state, extend=False, integrals=None):
'''
Calculate stresses at nodal points.
'''
# Point load.
mat = pb.get_materials()['Load']
P = 2.0 * mat.get_data('special', 'val')[1]
# Calculate nodal stress.
pb.time_update()
if integrals is None: integrals = pb.get_integrals()
stress = pb.evaluate('ev_cauchy_stress.ivn.Omega(Asphalt.D, u)', mode='qp',
integrals=integrals, copy_materials=False)
sfield = Field.from_args('stress', nm.float64, (3,),
pb.domain.regions['Omega'])
svar = FieldVariable('sigma', 'parameter', sfield,
primary_var_name='(set-to-None)')
svar.set_from_qp(stress, integrals['ivn'])
print('\n==================================================================')
print('Given load = %.2f N' % -P)
print('\nAnalytical solution')
print('===================')
print('Horizontal tensile stress = %.5e MPa/mm' % (-2.*P/(nm.pi*150.)))
print('Vertical compressive stress = %.5e MPa/mm' % (-6.*P/(nm.pi*150.)))
print('\nFEM solution')
print('============')
print('Horizontal tensile stress = %.5e MPa/mm' % (svar()[0]))
print('Vertical compressive stress = %.5e MPa/mm' % (-svar()[1]))
print('==================================================================')
return out
asphalt = materials['Asphalt'][0]
asphalt.update({'D' : stiffness_from_youngpoisson(2, young, poisson)})
options.update({'post_process_hook' : 'nodal_stress',})
integrals = {
'ivn' : ('custom', gdata.coors, [gdata.volume / nc] * nc),
}