acoustics/acoustics.py

Description

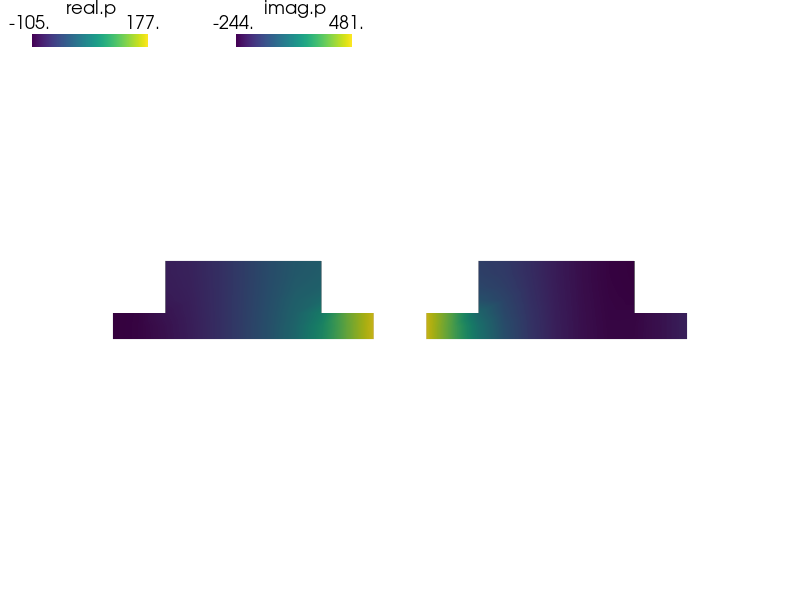
Acoustic pressure distribution.

This example shows how to solve a problem in complex numbers, note the ‘accoustic_pressure’ field definition.

Find such that:

source code

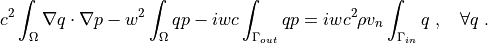
r"""
Acoustic pressure distribution.

This example shows how to solve a problem in complex numbers, note the
'accoustic_pressure' field definition.

Find :math:`p` such that:

.. math::
    c^2 \int_{\Omega} \nabla q \cdot \nabla p
    - w^2 \int_{\Omega} q p
    - i w c \int_{\Gamma_{out}} q p
    = i w c^2 \rho v_n \int_{\Gamma_{in}} q
    \;, \quad \forall q \;.
"""
from __future__ import absolute_import
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/2d/special/two_rectangles.mesh'

v_n = 1.0 # m/s
w = 1000.0
c = 343.0 # m/s
rho = 1.55 # kg/m^3

options = {
    'nls' : 'newton',
    'ls' : 'ls',
}

materials = {
    'one' : ({'one' : 1.0},),
}

regions = {
    'Omega' : 'all',
    'Gamma_in' : ('vertices in (x < 0.01)', 'facet'),
    'Gamma_out' : ('vertices in (x > 0.99)', 'facet'),
}

fields = {
    'accoustic_pressure' : ('complex', 1, 'Omega', 1),
}

variables = {
    'p'   : ('unknown field', 'accoustic_pressure', 0),
    'q'   : ('test field',    'accoustic_pressure', 'p'),
}

ebcs = {
}

integrals = {
    'i' : 2,
}

equations = {
    'Acoustic pressure' :
    """%s * dw_laplace.i.Omega( one.one, q, p )
    - %s * dw_dot.i.Omega( q, p )
    - %s * dw_dot.i.Gamma_out( q, p )
    = %s * dw_integrate.i.Gamma_in( q )"""
    % (c*c, w*w, 1j*w*c, 1j*w*c*c*rho*v_n)
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max'      : 1,
        'eps_a'      : 1e-1,
        'eps_r'      : 1.0,
        'macheps'   : 1e-16,
        'lin_red'    : 1e-1, # Linear system error < (eps_a * lin_red).
        'ls_red'     : 0.1,
        'ls_red_warp' : 0.001,
        'ls_on'      : 1.1,
        'ls_min'     : 1e-5,
        'check'     : 0,
        'delta'     : 1e-6,
    })
}