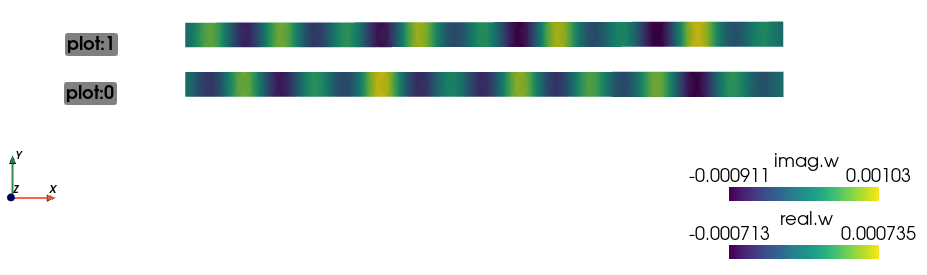Homogenization of the vibro-acoustic transmission on perforated plates with embedded resonators¶

Mathematical model¶

This example presents the implementation of the homogenized model of the acoustic transmission on perforated plates described in [RohanLukes2021]. The elastic plate interacting with an inviscid fluid is replaced by an interface on which the homogenized transmission conditions are applied, see Fig. 1.

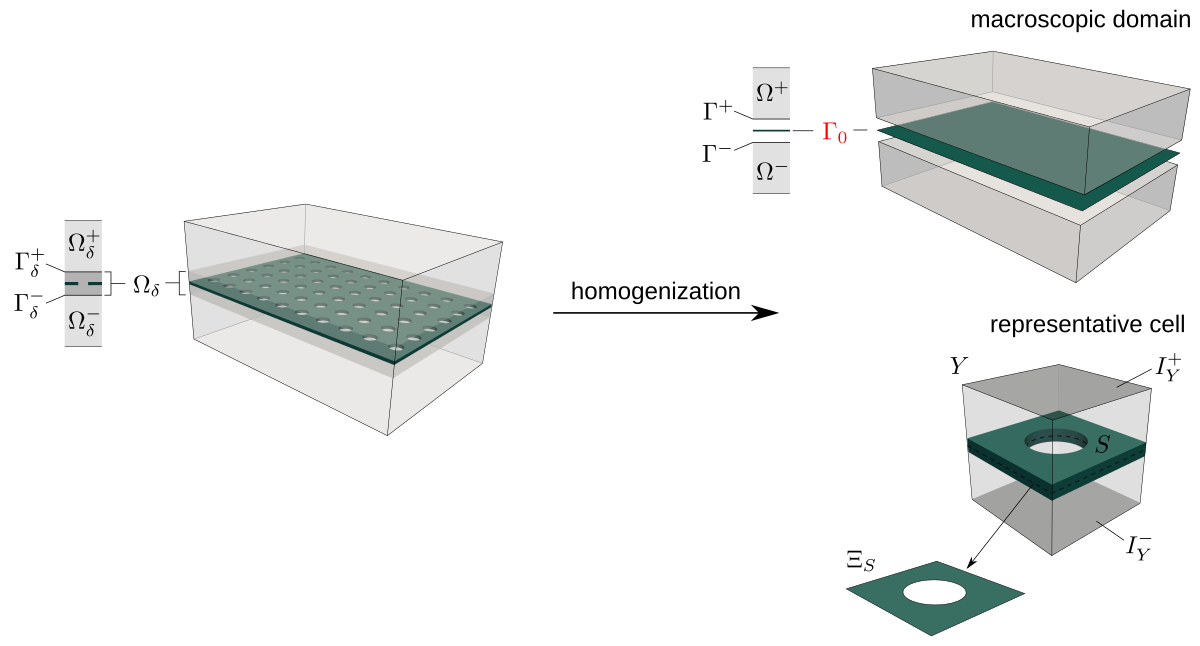
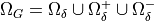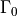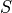Fig. 1 Transmission layer $\Omega_\delta$ of thickness $\delta$ embedded in the global domain $\Omega_G = \Omega_\delta \cup \Omega^+_\delta \cup \Omega^-_\delta$ is replaced by the homogenized interface $\Gamma_0$ . The solid part $S$ of the representative cell 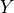$Y$ corresponds to the perforated plate.

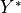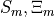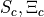The frequency dependent homogenized coefficients are computed using characteristic responses of the representative cell which consists of the fluid part $Y^\ast$ and the solid plate $S_m, \Xi_m$ embedding the elastic inclusion $S_c, \Xi_c$ and the resonator 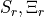$S_r, \Xi_r$ as illustrated in Fig. 2.

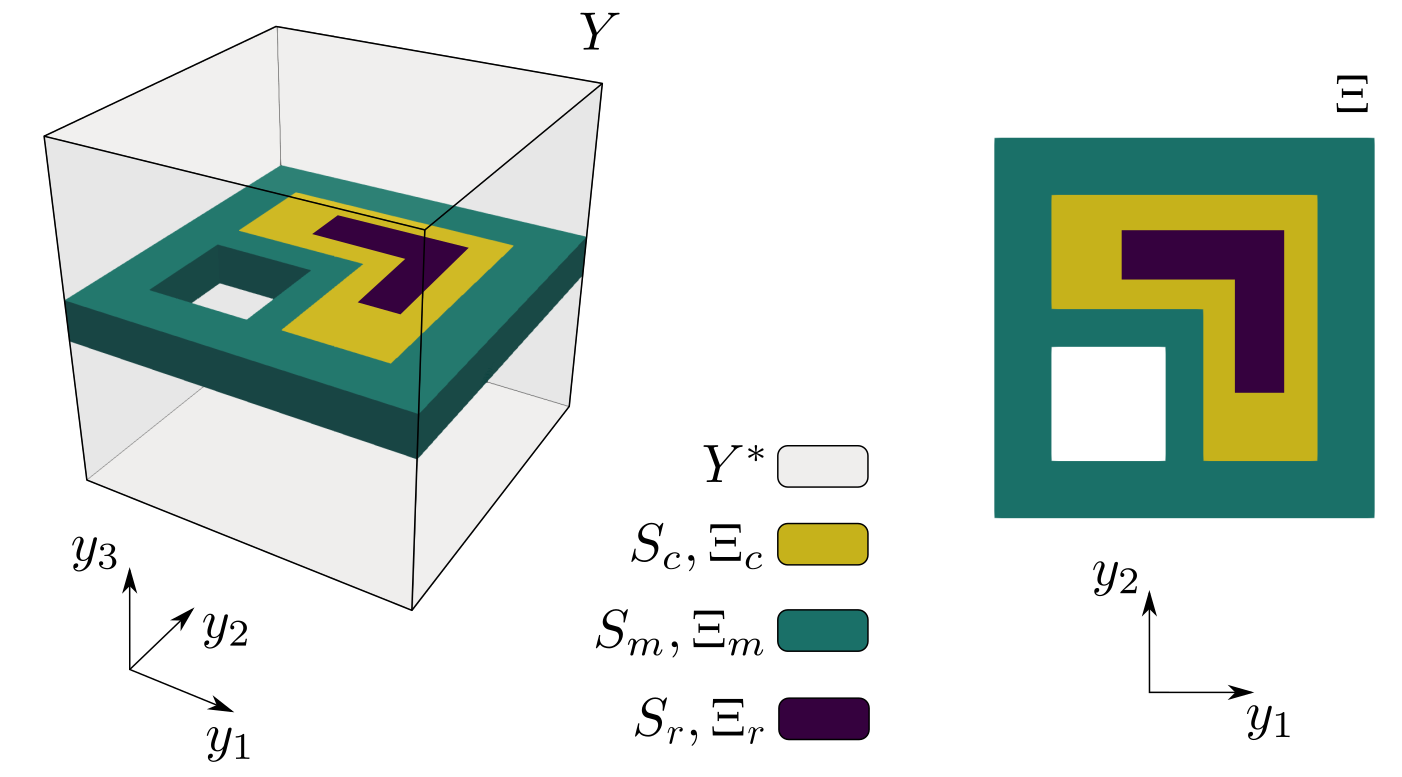
Fig. 2 The computational domains $Y$ and $\Xi$ involved in the calculations of the characteristic responses and the homogenized coefficients.

Equations describing the homogenized transmission layer involve the homogenized coefficients and are solved in the macroscopic domain $\Gamma_0$ and are coupled with the global acoustic field defined in $\Omega^+ \cup \Omega^-$ .

Numerical implementation¶

The problem of homogenized coefficients and the global macroscopic equations are discretized and solved by means of the finite element method. The frequency dependent coefficients are defined in acoustics_micro.py and the frequency independent coefficients calculated within the 2D plate representation $\Xi$ are specified in acoustics_micro_plate.py. The homogenization engine of SfePy, see [CimrmanLukesRohan2019], is employed for their effective calculation.

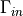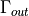At the macroscopic level, we consider the waveguide which domain is divided by the perforated plate into two parts of the same shape and size, see Fig. 3. The waveguide input is labelled by $\Gamma_{in}$ and the incident wave is imposed on this boundary. The anechoic boundary condition is considered at the waveguide output which is labelled by $\Gamma_{out}$ . The definition of the macroscopic problem is in files acoustics_macro.py and acoustics_macro_plate.py. 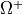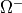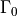The first file specifies the equations and variables related to $\Omega^+$ , $\Omega^-$ while the second one defines the equations associated with the homogenized interface $\Gamma_0$ .

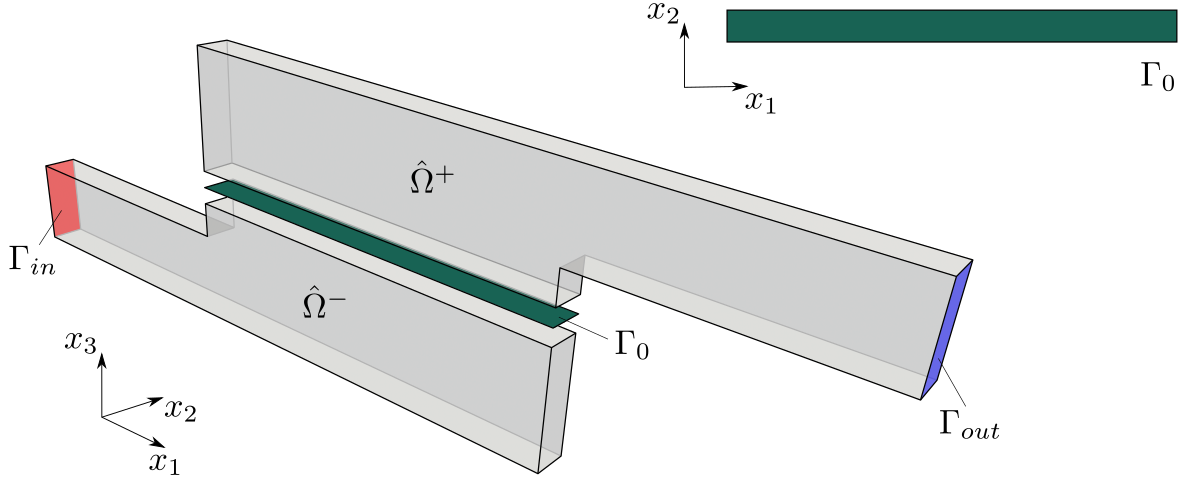
Fig. 3 The computational domains 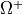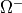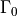$\Omega^+$ , $\Omega^-$ , $\Gamma_0$ employed in the numerical simulations of the acoustic transmission at the global (macroscopic) level.

The whole two-scale analysis is govern by the acoustics.py script which invokes the homogenization procedures and runs the simulation at the macroscopic level.

Running simulation¶

To run the numerical simulation, download the archive, unpack it in the main SfePy directory and type:

python example_vibroacoustics-2/acoustics.py

By running the resview.py script, you can visualize the distribution of the global pressure field calculated for frequency 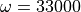$\omega = 33000$ Hz:

./resview.py example_vibroacoustics-2/results/waveguide_mesh_w33000_p.vtk -v "270,90"

Fig. 4 Distribution of the macroscopic pressure in the macroscopic domain $\Omega^+ \cup \Omega^-$ .

and e.g. the deflection field calculated at the interface 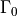$\Gamma_0$ :

./resview.py example_vibroacoustics-2/results/waveguide_mesh_w33000_dp0.vtk -v "0,0" --position-vector "0,2,0" -f real.w:p0 imag.w:p1

Fig. 5 Distribution of the plate deflection in the macroscopic domain $\Gamma_0$ .

References¶

[RohanLukes2021]

Rohan E., Lukeš V. Homogenization of the vibro-acoustic transmission on periodically perforated elastic plates with arrays of resonators. Applied Mathematical Modelling, 2022, DOI:10.1016/j.apm.2022.05.040

[CimrmanLukesRohan2019]

Cimrman R., Lukeš V., Rohan E. Multiscale finite element calculations in Python using SfePy. Advances in Computational Mathematics, 45(4):1897-1921, 2019, DOI:10.1007/s10444-019-09666-0
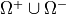