Multiscale numerical modelling of perfusion in deformable double porous media described by the Biot-Darcy-Brinkman model¶
Mathematical model¶
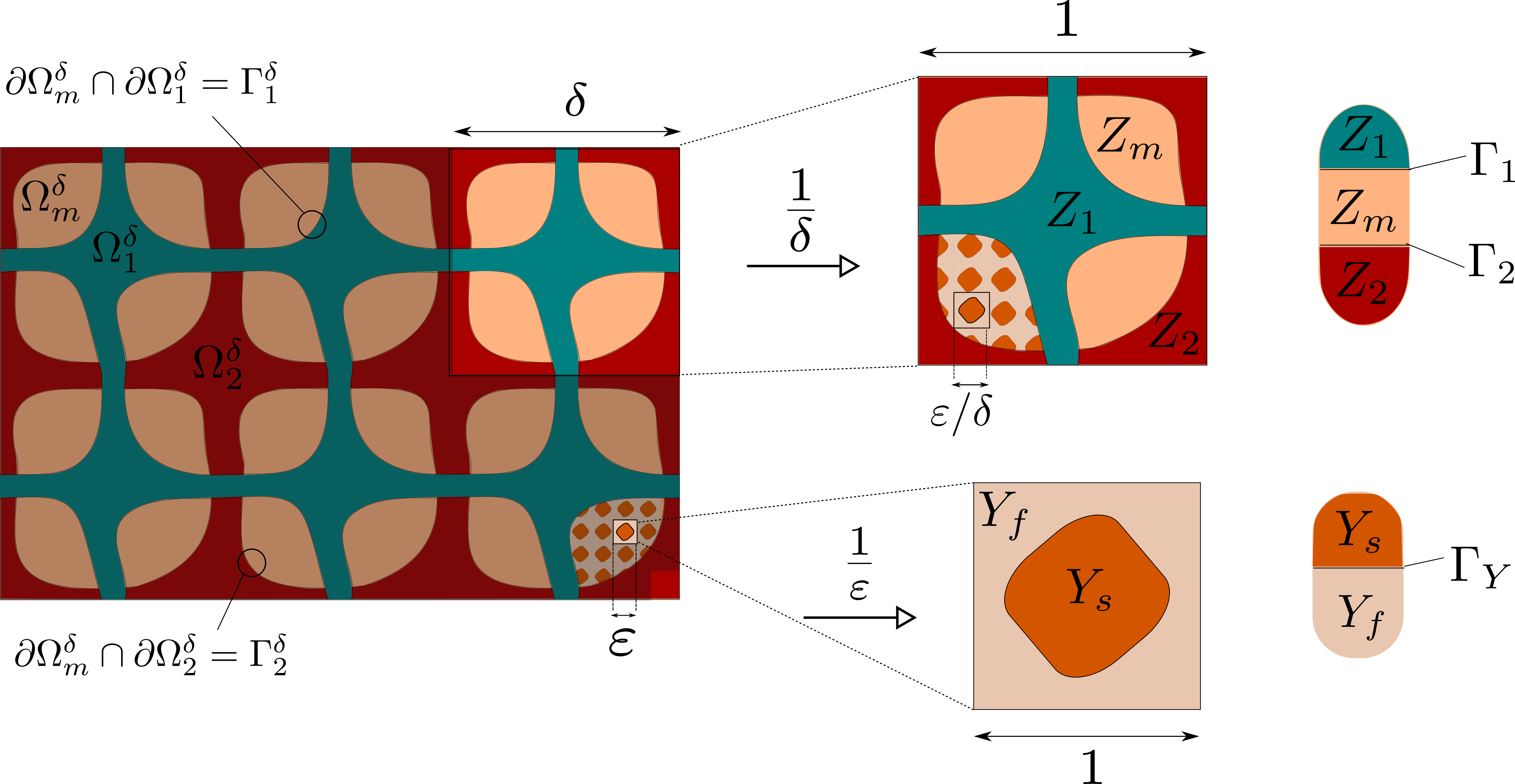
We consider a double porous medium which consists of an elastic solid matrix 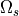 perforated by
a system of channels filled with an incompressible fluid
perforated by
a system of channels filled with an incompressible fluid 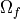 with interface
with interface
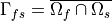 . These components are arranged in a periodic
lattice at both the micro- and mesoscopic level. Two small scale parameters
. These components are arranged in a periodic
lattice at both the micro- and mesoscopic level. Two small scale parameters  and
and 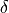 chracterize micro- and meso-porosities.
chracterize micro- and meso-porosities.
At the mesoscopic scale, the periodic structure is formed by two systems of fluid filled
channels occupying domains 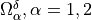 , whereby
, whereby 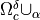 and by domain
and by domain 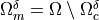 which is constituted by a microporous material.
In particular, domain
which is constituted by a microporous material.
In particular, domain 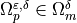 represents micro pores saturated by fluid,
whereas
represents micro pores saturated by fluid,
whereas 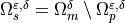 is the skeleton,
see Fig. 1.
is the skeleton,
see Fig. 1.
To summarize the decompositions,
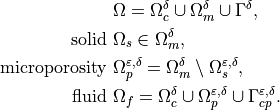
The mesoscopic channels 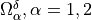 are mutually separated by the micro-porous matrix
are mutually separated by the micro-porous matrix
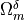 , so that also two disconnected interfaces are defined
, so that also two disconnected interfaces are defined
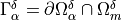 .
.
The microporous material is generated as a periodic lattice by repeating representative volume element (RVE) occupying
domain 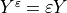 . It splits in the solid
. It splits in the solid 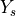 and fluid part
and fluid part 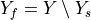 with interface
with interface 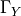 , as seen on Fig. 1.
, as seen on Fig. 1.
Similarly, at the mesoscopic level the porous structure is generated by RVE 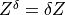 , with
decomposition into the part filled by microporous matrix
, with
decomposition into the part filled by microporous matrix 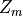 , and fluid channels
, and fluid channels 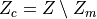 .
The channels further split into two sub-parts
.
The channels further split into two sub-parts 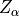 , each with interface
, each with interface
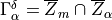 , see Fig. 1.
, see Fig. 1.
The superscripts  and
and  denote the quantities oscillating within the heterogeneous
structure with the period equal to the size of the micro- and mesoscopic periodic unit. However, we drop the superscript
in following text to simplify the notation.
denote the quantities oscillating within the heterogeneous
structure with the period equal to the size of the micro- and mesoscopic periodic unit. However, we drop the superscript
in following text to simplify the notation.
The mechanical behavior of such a structure can be described using the two-level asymptotic homogenization method, (for more detailed explanaition we refer to [RohanTurjanicovaLukes2020]).
The mechanical properties of the deformable matrix are given by elasticity tensor 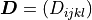 which satisfies
the usual symmetries.
which satisfies
the usual symmetries.
The fluid is characterized by viscosity 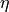 which is given by a piece-wise constant function,
which is given by a piece-wise constant function,
(1)¶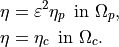
The scaling of the viscosity in micropores  is the standart consequence of the non-slip boundary
condition on he pore wall.
is the standart consequence of the non-slip boundary
condition on he pore wall.
The problem of the fluid flow in deformable media at microscopic level is given by the following
equilibrium equations and boundary conditions governing displacement of the solid  and both the fluid
pressure and velocity fields
and both the fluid
pressure and velocity fields  :
:
(2)¶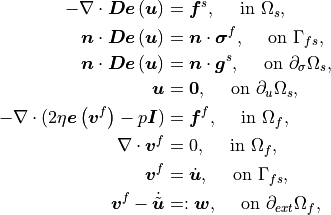
where 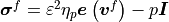 is the fluid stress,
is the fluid stress, 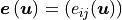 is the strain in the solid with components
is the strain in the solid with components 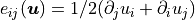 ,
, 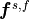 denotes the volume forces in the solid or in the fluid, and
denotes the volume forces in the solid or in the fluid, and 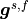 is the surfacetraction stresses acting
on the solid part. The relative fluid velocity
is the surfacetraction stresses acting
on the solid part. The relative fluid velocity 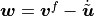 in the fluid-filled pores
in the fluid-filled pores
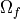 is defined whit use of a smooth extention
is defined whit use of a smooth extention 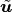 of the dislacement field
of the dislacement field 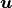 from solid
from solid 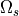 to whole domain
to whole domain 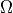 .
.
Two-level homogenization¶
Due to the double-porous nature of the medium, we performe two levels of homogenization.
The 1st-level of homogenization concerns the asymptotic analysis 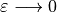 related to the
fluid-structure interaction in microporous structure situated in
related to the
fluid-structure interaction in microporous structure situated in 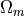 .
We apply the standard homogenization techniques to the above problem. It
results in the limit model for
.
We apply the standard homogenization techniques to the above problem. It
results in the limit model for 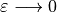 , where
, where
 is the scale parameter relating the microscopic and macroscopic
length scales. The homogenization process leads to local microscopic problems,
defined within a reference periodic cell
is the scale parameter relating the microscopic and macroscopic
length scales. The homogenization process leads to local microscopic problems,
defined within a reference periodic cell 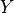 , and to the mesoscopic problem describing
the behavior of the homogenized matrix at the mesoscopic level. The mesoscopic
problem involves the homogenized material coefficients which are evaluated
using the solutions of the local problems. The 2nd-level of homogenization deals with upsacling from meso-
to macroscopic scale. It results in the limit model for
, and to the mesoscopic problem describing
the behavior of the homogenized matrix at the mesoscopic level. The mesoscopic
problem involves the homogenized material coefficients which are evaluated
using the solutions of the local problems. The 2nd-level of homogenization deals with upsacling from meso-
to macroscopic scale. It results in the limit model for
 and subsequently in the local mesoscopic problems on
a reference periodic cell
and subsequently in the local mesoscopic problems on
a reference periodic cell 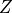 , and in the derivation of the homogenized problem at macroscopic level.
Due to linearity of the problem, the microscopic, mesoscopic and macroscopic problems are decoupled.
, and in the derivation of the homogenized problem at macroscopic level.
Due to linearity of the problem, the microscopic, mesoscopic and macroscopic problems are decoupled.
The local microscopic responses are given by the following sub-problems which are solved within the periodic
reference cell 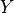 , see Fig. 1, that is decomposed similarly to the decomposition of
domain
, see Fig. 1, that is decomposed similarly to the decomposition of
domain 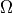 :
:
- Find
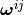 ,
, 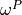 such that for all
such that for all 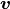 for any
for any 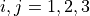
(3)¶![\int_{Y_s} \Db \eeby{\omegab^{ij} + \Pib^{ij}}: \eeby{\vb}\,\dV &= 0, \\
\int_{Y_{s}} \Db \eeby{\omegab^P}: \eeby{\vb}\,\dV &=
-{1\over \vert Y\vert}\int_{\Gamma_Y} \vb \cdot \nb^{[s]}\, \dS,](_images/math/b866fd6c94aedfc1759c480260836d989d7448ef.png)
where 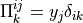 .
.
- Find
 ,
, 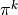 such that for all
such that for all 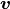 ,
,
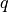 satisfying
satisfying
(4)¶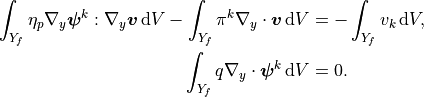
The microscopic sub-problems are solved with the periodic boundary conditions
and 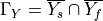 is the interface between solid and fluid part of the cell
is the interface between solid and fluid part of the cell 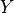 .
.
With the characteristic responses obtained by solving local sub-problems,
the homogenized material coefficients 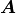 ,
, 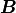 ,
, 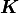 and
and 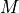 can be evaluated
using the following expressions:
can be evaluated
using the following expressions:
(5)¶![A_{ijkl} & = {1\over \vert Y\vert} \left[ \int_{Y_{s}} \Db \eeby{\omegab^{kl} + \Pib^{kl}}: \eebz{\omegab^{ij} + \Pib^{ij}}\,\dV\right],\\
B_{ij} & = \phi_f\delta_{ij}-{1\over \vert Y\vert} \left[\int_{Y_s} \Db \eeby{\omegab^{P}}:\eeby{\Pib^{ij}}\,\dV\right],\\
K_{ij} & = {1\over \vert Y\vert} \int_{Y_f} \nabla_y\psi^i:\nabla_y\psi^i\,\dV,\\
M & = {1\over \vert Y\vert} \left[\int_{Y_s} \Db \eeby{\omegab^{P}}:\eeby{\omegab^{P}} \,\dV \right].](_images/math/58053c190167aeaeeec9e092cb72cf3f361f1399.png)
Homogenization - 2nd level¶
At the 2st-level of homogenization, the asymptotic analysis  is related to the
interaction between the homogenized microporous matrix in
is related to the
interaction between the homogenized microporous matrix in 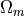 and fluid in channels
and fluid in channels 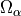 at mesoscopic level. By similar upscaling procedure as in 1st level of homogenization, we obtain
local mesoscopic problems,
defined within a reference periodic cell
at mesoscopic level. By similar upscaling procedure as in 1st level of homogenization, we obtain
local mesoscopic problems,
defined within a reference periodic cell 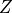 ,
where we enter the homogenized coefficients obtained by 1st level homogenization. However, when compared to the model
of a mesoscopic structure containing only one system of channels, the upscaled mesoscopic structures involving
two mesoscopic channels yields two macroscopic velocity fields
,
where we enter the homogenized coefficients obtained by 1st level homogenization. However, when compared to the model
of a mesoscopic structure containing only one system of channels, the upscaled mesoscopic structures involving
two mesoscopic channels yields two macroscopic velocity fields 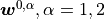 which describe the
two parallel flows.
which describe the
two parallel flows.
We also arrive to the global problem describing the behavior of the homogenized matrix at the macroscopic level. The homogenized material coefficients describing whichdescribe behavior at macroscopic level are evaluated using the solutions of the local mesoscopic problems.Due to linearity of the problem, the microscopic, mesoscopic and macroscopic problems are decoupled.
The local mesoscopic responses are given by the following sub-problems which are solved within the periodic
reference cell 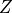 , see Fig. 1, that is decomposed similarly to the decomposition of
domain
, see Fig. 1, that is decomposed similarly to the decomposition of
domain 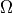 :
:
- Find
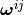 ,
, 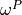 such that for all
such that for all 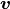 for any
for any 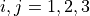
(6)¶![\int_{Z_m} \Ab \eebz{\omegab^{ij} + \Pib^{ij}}: \eebz{\vb}\,\dV &= 0, \\
\int_{Z_{m}} \Ab \eebz{\omegab^P}: \eebz{\vb}\,\dV - \int_{Z_m} \Bb: \eebz{\vb} \,\dV &=
-{1\over \vert Z\vert}\int_{\Gamma_z} \vb \cdot \nb^{[m]}\, \dS ,](_images/math/37b24f8feb7c13f3db020b3dd32a97a7c9dab7ca.png)
where 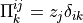 .
.
- Find
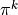 ,
, 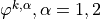 such that for all
such that for all 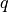 satisfying
satisfying
(7)¶![\int_{Z_{m}} \nabla_z q \Kb \nabla_z \pi^k \,\dV &= -\int_{Z_{m}} \nabla_z q \Kb \nabla_z z_k , \\
\int_{Z_{m}} \nabla_z q \Kb \nabla_z \vphi^{k,\alpha} \,\dV &= {1\over \vert Z\vert}\int_{\Gamma^Z_\alpha} q \nb^{[c]}_k\, \dS .](_images/math/7c0ee31763c788ab5b25b91d25da4636aeb19c80.png)
- Find
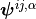 ,
, 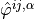 such that for all
such that for all 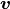 ,
,
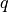 satisfying
satisfying
(8)¶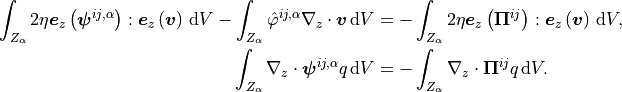
The mesoscopic sub-problems are solved with the periodic boundary conditions
and 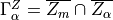 is the interface between
the matrix part
is the interface between
the matrix part 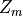 and system of channels
and system of channels 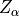 .
.
With the characteristic responses obtained by solving local sub-problems,
the homogenized material coefficients 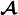 ,
, 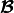 ,
, 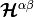 ,
, 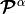 ,
,
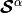 , and
, and 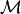 can be evaluated
using the following expressions:
can be evaluated
using the following expressions:
(9)¶![\Acal_{ijkl} & = {1\over \vert Z\vert} \left[ \int_{Z_{m}} \left[\Ab \eebz{\omegab^{kl}
+ \Pib^{kl}}\right]: \eebz{\omegab^{ij} + \Pib^{ij}}\,\dV\right],\\
\Bcal_{ij} & = \phi_c\delta_ij+{1\over \vert Z\vert} \left[\int_{Z_m} \Bb: \eebz{\Pib^{ij}+\omegab^{ij}} \,\dV
- \int_{\Gamma_Z} \nb^{m}\cdot \omegab^{ij} \,\dV\right],\\
\Hcal^{\alpha\beta}_{ij} & = {1\over \vert Z\vert} \int_{Z_m} \nabla_z\vphi^{j,\beta}\cdot\Kb\nabla_z\vphi^{i,\alpha}\,\dV,\\
\Kcal_{ij} & = {1\over \vert Z\vert} \int_{Z_m} \nabla_z(z_j+\pi^j)\cdot\Kb\nabla_z(z_i+\pi^i)\,\dV,\\
\Pcal^\alpha_{ij} &= \phi_\alpha\delta_{ij}-{1\over \vert Z\vert}\int_{\Gamma_Z} \pi^i n_j^{\alpha}\, \dS
=\phi_\alpha\delta_{ij}+{1\over \vert Z\vert} \int_{Z_m} \nabla_z\pi^i\cdot\Kb\nabla_z\vphi^{j,\alpha}\,\dV,\\
\Scal^\alpha_{{ijkl}} &={1\over \vert Z\vert}\left[2\eta\int_{Z_\alpha}\eebz{\psib^{kl}+\Pib^{kl}}:\eebz{\psib^{ij}
+\Pib^{ij}}\,\dV-\int_{Z_c} \hat{\vphi}^{kl}\nabla_z\cdot\Pib^{ij}\, \dV\right],\\
\Mcal &={1\over \vert Z\vert}\left[\int_{Z_m}M\,\dV+ \int_{Z_m} \Bb: \eebz{\omegab^{P}} \,\dV
- \int_{\Gamma_Z} \nb^{c}\cdot \omegab^{P} \,\dV\right].](_images/math/4c4acbc1ff5a30e4657d5a089517dc2b18c3dfa9.png)
All coefficients are symmetric with respect to indices related to strain and strain rate tensors, i.e. 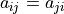 .
.
The global macroscopic problem is defined in terms of the homogenized
coefficients as: Find the macroscopic displacements 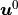 , pressure
, pressure
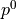 and velocity fields
and velocity fields 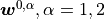 such that for all
such that for all 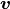 ,
, 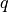 and
and 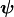
(10)¶![\int_{\Omega} \left[\Acalb \eebx{\ub^0} - p^0 \Bcalb^T\right]: \eebx{\vb}\,\dV
- \sum\limits_\alpha \int_{\Omega}\vb\cdot \left[(\Pcalb^\alpha)^T(\nabla_xp^0-\fb^f)
+ \sum\limits_{\beta=1,2} \Hcalb^{\alpha\beta}\wb^{0,\beta}\right]&\,\dV +\int_{\partial_\sigma\Omega}\bar{\phi}_c\bar{p^0}\nb\cdot\vb^0\,\dV\\
&= \int_{\Omega} \fb^{blk}\cdot\vb \,\dV+\int_{\partial_\sigma\Omega}\bar{\phi}_m\bar{\phi}_s\gb\cdot\vb\,\dV,
+ \int_{\Omega} \fb^f \cdot \vb \dV,\\
\int_{\Omega} q\left[\Bcalb:\eebx{\dot\ub^0} + \dot p^0 \Mcal\right] \dV
+\int_\Omega \nabla q\cdot \left[\Kcalb(\nabla_xp^0-\fb^f)-\sum\limits_{\beta=1,2}\Pcalb^\beta\wb^{0,\beta}\right]\,\dV
&= -\int_{\partial_w\Omega} q (\bar\phi_m\bar\phi_f\bar w_n^{mic}+\sum\limits_{\beta=1,2}\bar\phi_\beta\bar w_n^{mes,\beta}) \,\dV,\\
\int_{\Omega}\eebx{\psib}:\Scalb^\alpha\eebx{\wb^{0,\alpha}+\dot\ub^0}\,\dV
+\int_\Omega\psib\cdot\left[(\Pcalb^\alpha)^T(\nabla_xp^0-\fb^f) + \sum\limits_{\beta=1,2} \Hcalb^{\alpha\beta}\wb^{0,\beta} \right]\,\dV&=0.](_images/math/fd0e5c8327270acbcfd0ac2a1e668bcd24994c22.png)
The Dirichlet boundary conditions prescribed for 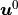 and
and 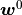 can be imposed,
can be imposed,
(11)¶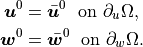
The pressure 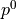 fulfils zero-means conditions
fulfils zero-means conditions 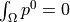 in the whole domain
in the whole domain 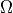 .
.
The complementary Neumann-type boundary condition are specfied as follows
(12)¶![\nb\cdot\left[\Acalb \eebx{\ub^0} - p^0 \Bcalb^T\right]&=-\bar{\phi}_c\bar{p^0}\nb+\bar{\phi}_m\bar{\phi}_s\gb=\0b
\; \textrm{ on }\partial_\sigma\Om,\\
\nb\cdot\left[\Kcalb(\nabla_x p^0-\fb^f)-\sum\limits_{\beta=1,2}\Pcalb^\beta \wb^{0,\beta}\right]&=
\bar\phi_m\bar\phi_f\bar w_n^{mic}+\sum\limits_{\beta=1,2}\bar\phi_\beta\bar w_n^{mes,\beta}
\; \textrm{ on }\partial_j\Om,\\
\nb\cdot\Scalb^\alpha\eebx{\wb^{0,\alpha}+\dot\ub^0}&=\bar\phi_\alpha P^0_\alpha\nb=\0b\; \textrm{ on }\partial_p\Om.](_images/math/629c868393a545af7fe15100ad4a45b1eeb7b0c2.png)
For the purpose of this example, we simplify the problem (13). We omitt all volume froces
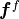 and
and 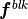 and surface tractions
and surface tractions 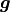 . Also we will consider
closed micropores on the whole boundary
. Also we will consider
closed micropores on the whole boundary 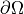 , i.e.
, i.e. 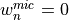 .
The problem (10) becomes:
Find the macroscopic displacements
.
The problem (10) becomes:
Find the macroscopic displacements 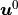 , velocity
, velocity 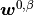 and pressure fields
and pressure fields
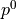 such that for all
such that for all 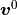 ,
, 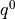 and
and 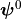
(13)¶![\int_{\Omega} \left[\Acalb \eebx{\ub^0} - p^0 \Bcalb^T\right]: \eebx{\vb}\,\dV
- \sum\limits_\alpha \int_{\Omega}\vb\cdot \left[(\Pcalb^\alpha)^T(\nabla_xp^0-\fb^f)
+ \sum\limits_{\beta=1,2} \Hcalb^{\alpha\beta}\wb^{0,\beta}\right]\,\dV &= 0,\\
\int_{\Omega} q\left[\Bcalb:\eebx{\dot\ub^0} + \dot p^0 \Mcal\right] \dV
+\int_\Omega \nabla q\cdot \left[\Kcalb(\nabla_xp^0-\fb^f)-\sum\limits_{\beta=1,2}\Pcalb^\beta\wb^{0,\beta}\right]\,\dV
&= -\int_{\partial_w\Omega} q \sum\limits_{\beta=1,2}\bar\phi_\beta\bar w_n^{mes,\beta} \,\dV,\\
\int_{\Omega}\eebx{\psib}:\Scalb^\alpha\eebx{\wb^{0,\alpha}+\dot\ub^0}\,\dV
+\int_\Omega\psib\cdot\left[(\Pcalb^\alpha)^T(\nabla_xp^0-\fb^f) + \sum\limits_{\beta=1,2} \Hcalb^{\alpha\beta}\wb^{0,\beta} \right]\,\dV&=0.](_images/math/98095cfcad47e01807943cead25b440f51ed0d3a.png)
The initial conditions of fields 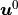 and
and 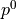 are necessary for computation of time dependent problem
and are computed using the steady state form of the boundary problem defined above.
are necessary for computation of time dependent problem
and are computed using the steady state form of the boundary problem defined above.
Numerical simulation¶
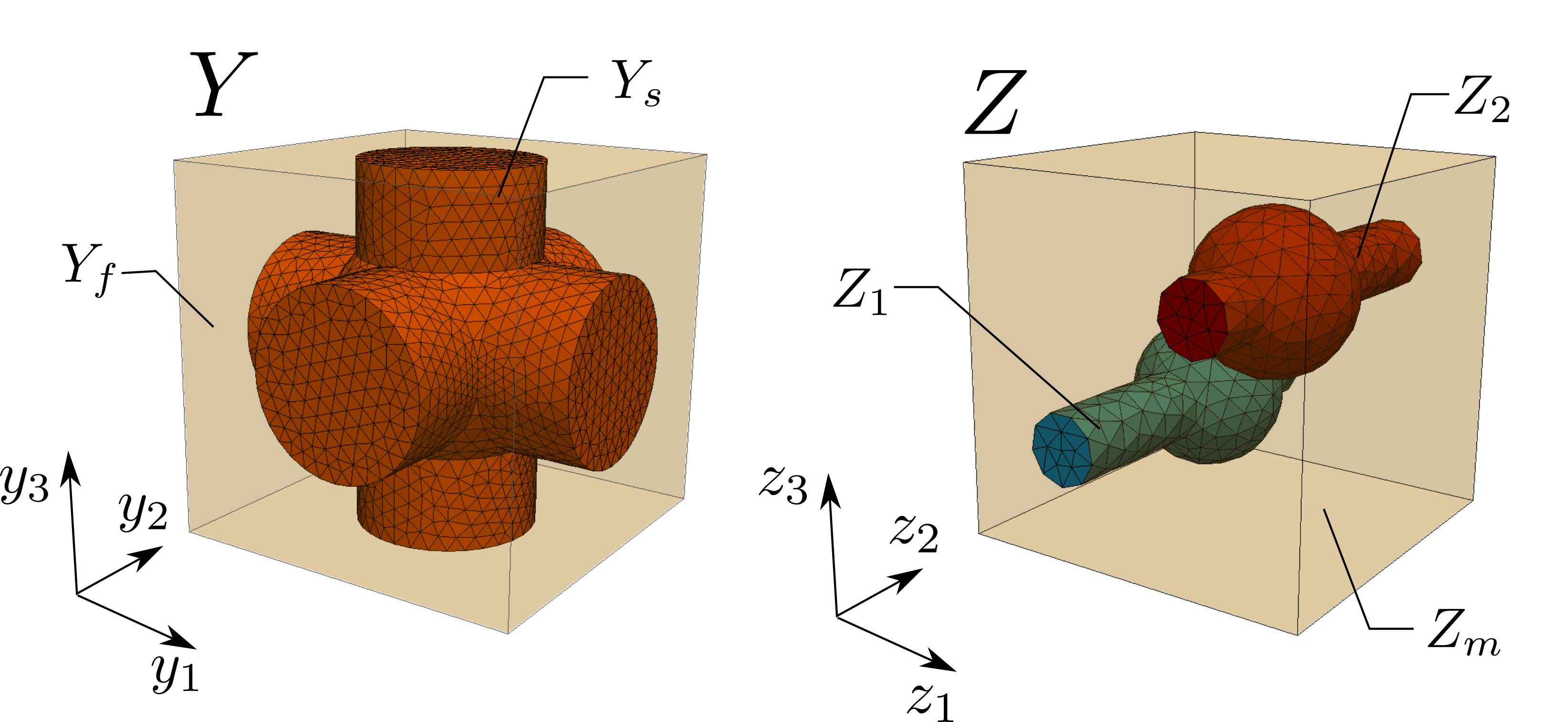
Fig. 2 Left - geometric representation of microscopic domain; Right - geometric representation of mesoscopic domain
To run the numerical simulation, download the archive, unpack it in the main SfePy directory and type:
./simple.py example_perfusion_BD2B-1/perf_BD2B_mac.py
This invoke the simply.py script which calculates the macroscopic
problem (13) and calls the homogenization engine that solves the
local subproblems for given parameter  , viscosity
, viscosity 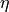 and elastic tensor
and elastic tensor 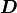 . First, it solves subproblems (3) and (4)
on microscopic cell
. First, it solves subproblems (3) and (4)
on microscopic cell 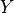 (see Fig. 2 left) and
evaluates the homogenized
coefficients (5). Then, using solution from previous step, it solves subproblems
(6)–(8) on mesoscopic cell
(see Fig. 2 left) and
evaluates the homogenized
coefficients (5). Then, using solution from previous step, it solves subproblems
(6)–(8) on mesoscopic cell 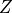 (see Fig. 2 right)
and evaluates the homogenized coefficients (9). See [CimrmanLukesRohan2019] for more details related
to the SfePy homogenization engine.
(see Fig. 2 right)
and evaluates the homogenized coefficients (9). See [CimrmanLukesRohan2019] for more details related
to the SfePy homogenization engine.
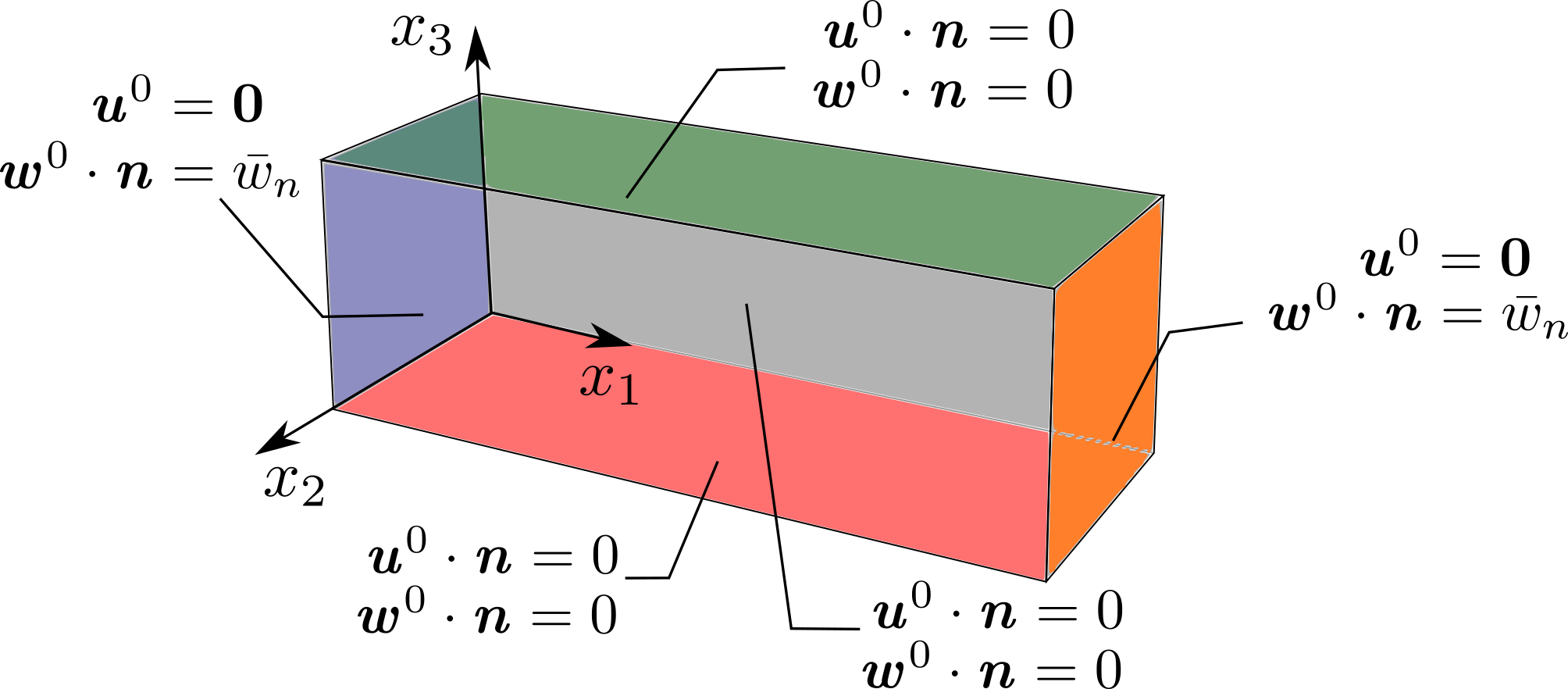
Then, the script computes both the steady state and time evolution of the problem (13). For steady
state, the macroscopic sample is fixed on both top and bottom side, so that no displacements are
allowed, see Fig. 3. The defromation is induced due to the flow through porous matrix, as the
responce to the prescribed velocities 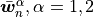 , see (13).
, see (13).
For simulation of the time evolution of the macroscopic problem we take the steady state as initial value of displacement and preassure fields. In this case, the gradually increasing displacement is prescribed on the top side of the macroscopic sample.
The resulting macroscopic pressure field 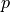 , displacement
, displacement 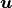 and the velocity fields
and the velocity fields
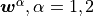 are depicted in Fig. 4, Fig. 5
and Fig. 4. These figures depict distribution of macroscopic quantities on
the deformingin at macroscopic specimen at different computational times
(
are depicted in Fig. 4, Fig. 5
and Fig. 4. These figures depict distribution of macroscopic quantities on
the deformingin at macroscopic specimen at different computational times
(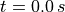 ,
, 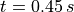 and
and 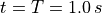 ). The nondeformed shape of macroscopic specimen is
visualised by its outline.
). The nondeformed shape of macroscopic specimen is
visualised by its outline.

Fig. 4 Macroscopic sample and the resulting macroscopic fields: left - displacement
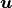 field at different computational times; right - pressure
field at different computational times; right - pressure
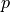 field at different computational times.
field at different computational times.
References¶
| [RohanTurjanicovaLukes2020] | Rohan E., Turjanicová J., Lukeš V. Multiscale modelling and simulations of tissue perfusion using the Biot-Darcy-Brinkman model. Submitted to Computers & Structures, 2020 |
| [CimrmanLukesRohan2019] | Cimrman R., Lukes V., Rohan E. Multiscale finite element calculations in Python using SfePy. Advances in Computational Mathematics, 45(4):1897-1921, 2019, DOI:10.1007/s10444-019-09666-0 |
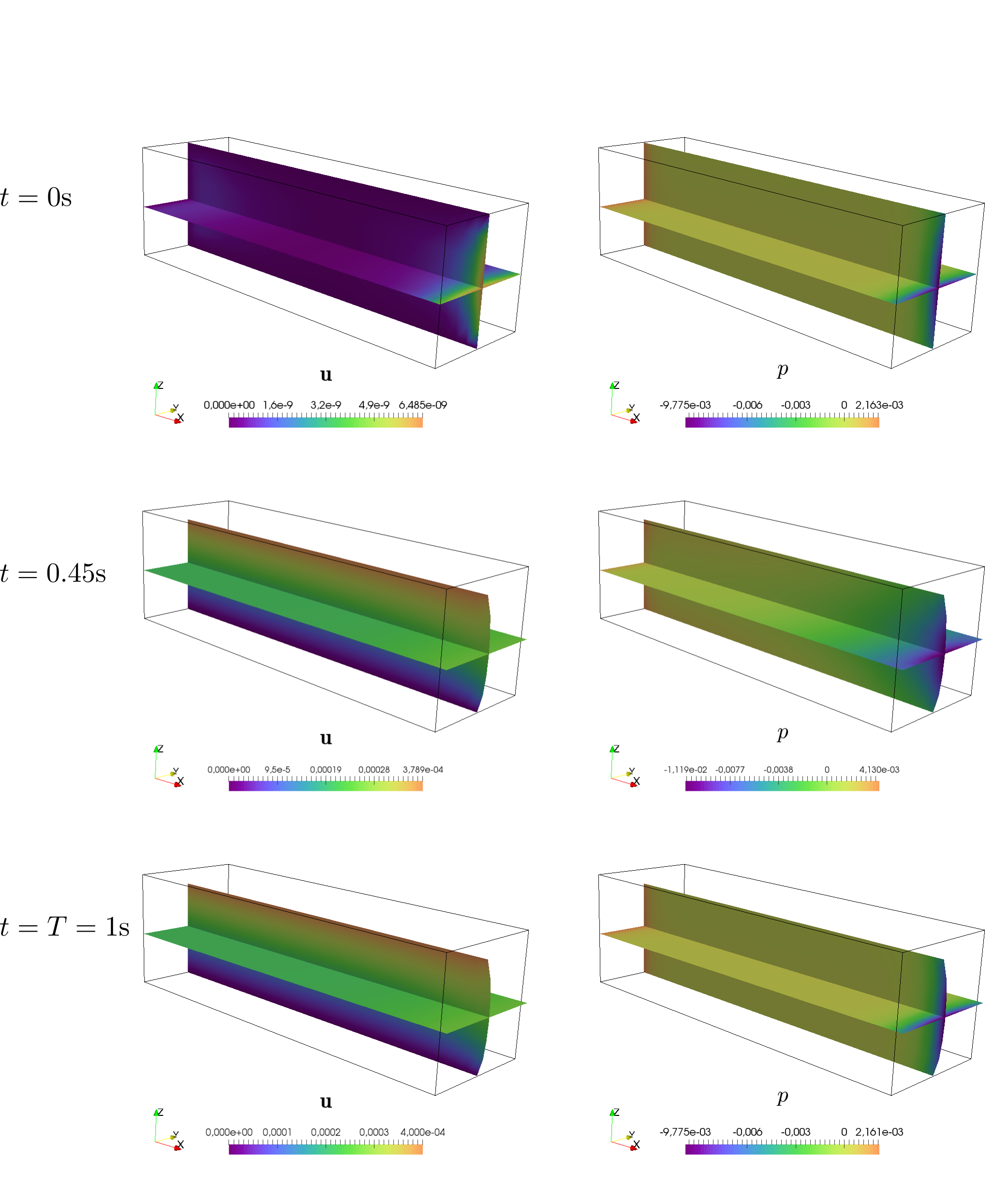
 -crosssection at different computational times; right - pressure
-crosssection at different computational times; right - pressure
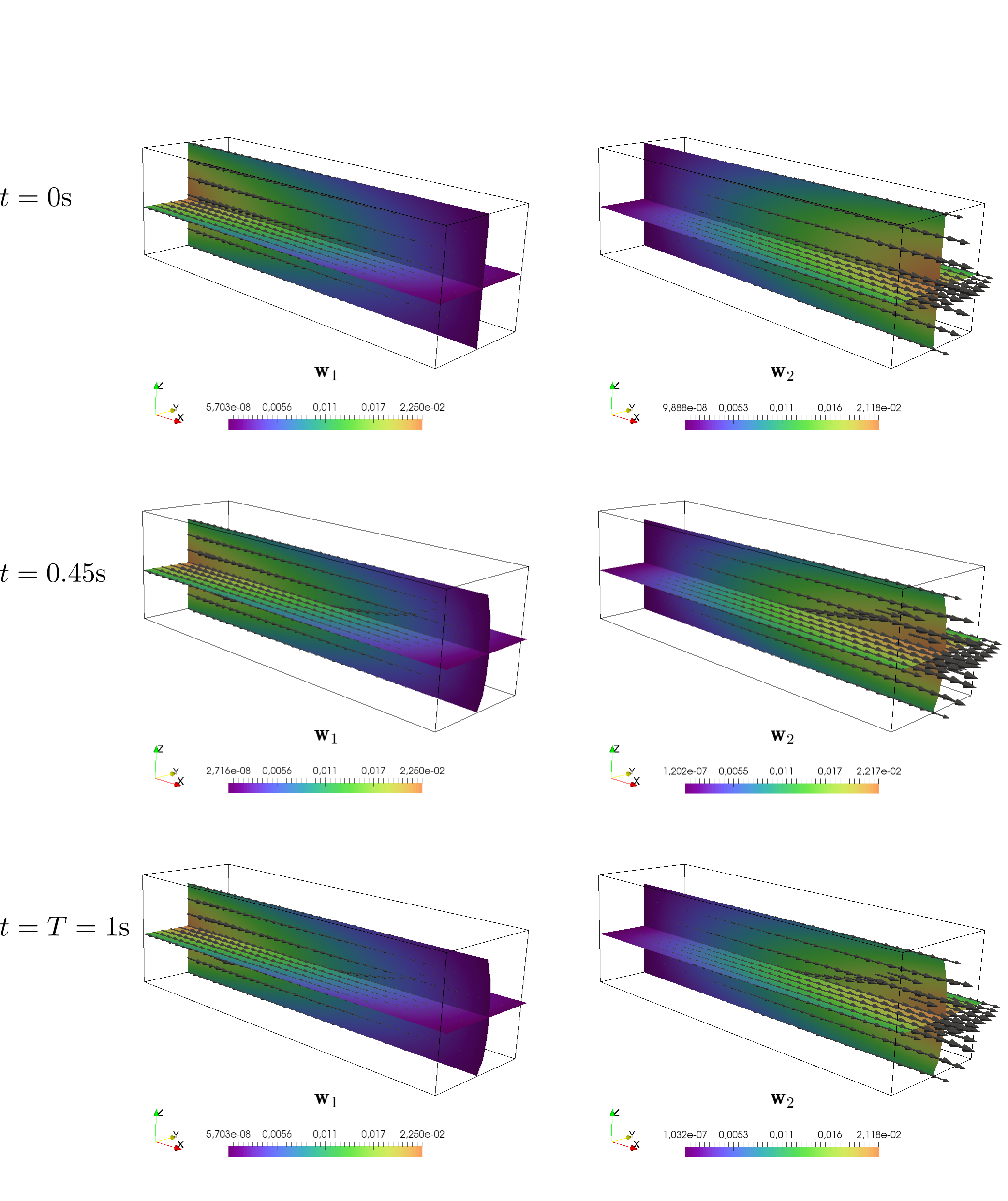
 in
in 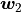 in
in