Two-scale numerical simulation of a large deforming fluid-saturated porous structure¶
Mathematical model¶
We consider a fluid-saturated porous medium undergoing large deformations. A double porous medium is constituted by a hyperelastic skeleton and an incompressible viscous fluid. Within the Eulerian framework related to the current deformed configuration, the two-scale homogenization approach is applied to a linearized model discretized in time, being associated with an incremental formulation. The homogenization procedure of the linearized equations provides effective (homogenized) material properties which are computed to constitute the incremental macroscopic problem. The multiscale model is derived and discussed in [LukesRohan2022].
Implementation¶
The local subproblems defined within the reference cell and the global
macroscopic equations are discretized and solved by means of the finite element
method. The macroscopic equations and the incremental ULF algorithm are defined
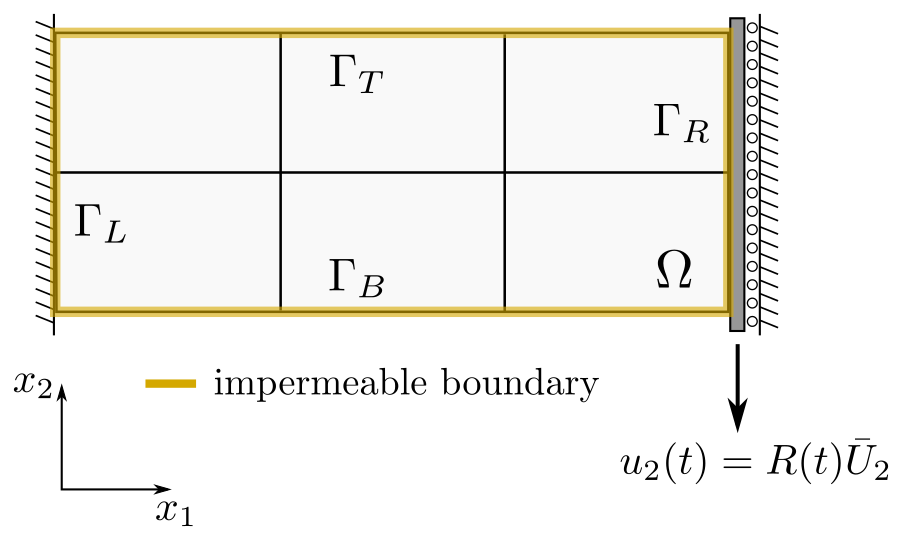
in largedef_porous_mac.py. The finite element mesh representing the
macroscopic domain and the applied boundary conditions are depicted in
Fig. 1.
The local microscopic problems and the homogenized coefficients are specified
in largedef_porous_mic.py. The domain, on which the microscopic
calculations are performed, is shown in Fig. 2. It consists of the
porous matrix  and two fluid channels
and two fluid channels  ,
,  .
.
The macro-micro coupling is governed by the SfePy homogenization engine, see [CimrmanLukesRohan2019], which ensures efficient evaluation of the homogenized coefficients demanded by the macroscopic simulation.
Running simulation¶
To run the multiscale numerical simulation, download the archive, unpack it in the main SfePy directory and type:
./simple.py example_largedef_porous-1/largedef_porous_mac.py
This invokes the time-stepping solver for the problem at the macroscopic level
which calls the homogenization engine evaluating the homogenized coefficients
defined in largedef_porous_mic.py. The coefficients are evaluated in
several embedded loops associated with the time steps and the macroscopic
integration points, see [LukesRohan2022] for details.
The computed macroscopic results can be visualized using the resview.py
post-processing script as follows:
./resview.py example_largedef_porous-1/results/macro_mesh_3x2_*.vtk -w u0 -f cauchy_stress:p0 -v "0,0" -s 18
References¶
| [LukesRohan2022] | (1, 2) Lukeš V., Rohan E. Homogenization of large deforming fluid-saturated porous structures. Computers and Mathematics with Applications, 110:40-63, 2022, DOI:10.1016/j.camwa.2022.01.036 |
| [CimrmanLukesRohan2019] | Cimrman R., Lukeš V., Rohan E. Multiscale finite element calculations in Python using SfePy. Advances in Computational Mathematics, 45(4):1897-1921, 2019, DOI:10.1007/s10444-019-09666-0 |
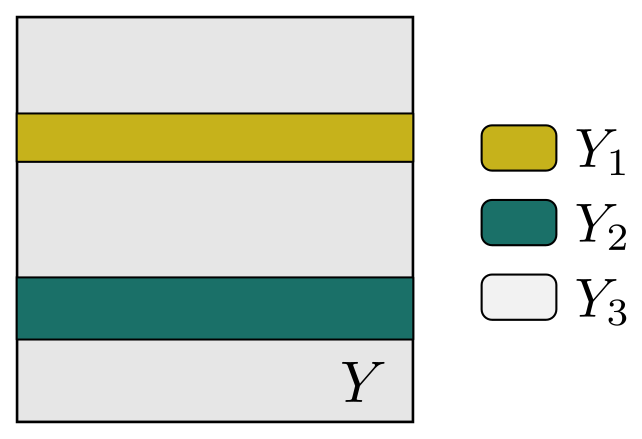
 .
.