sfepy.terms.terms_hyperelastic_tl module¶
- class sfepy.terms.terms_hyperelastic_tl.BulkActiveTLTerm(*args, **kwargs)[source]¶
Hyperelastic bulk active term. Stress
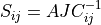 ,
where
,
where 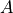 is the activation in
is the activation in ![[0, F_{\rm max}]](../../../_images/math/df8916b59bfe535d73f8f15fcf975958474edbe7.png) .
.- Definition:
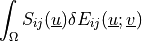
- Call signature:
dw_tl_bulk_active
(material, virtual, state)- Arguments:
material :
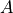
virtual :

state :

- family_data_names = ['det_f', 'sym_inv_c']¶
- name = 'dw_tl_bulk_active'¶
- static stress_function(out, mat, det_f, vec_inv_cs)¶
- static tan_mod_function(out, mat, det_f, vec_inv_cs)¶
- class sfepy.terms.terms_hyperelastic_tl.BulkPenaltyTLTerm(*args, **kwargs)[source]¶
Hyperelastic bulk penalty term. Stress
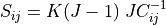 .
.- Definition:
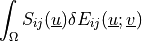
- Call signature:
dw_tl_bulk_penalty
(material, virtual, state)- Arguments:
material :
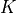
virtual :

state :

- family_data_names = ['det_f', 'sym_inv_c']¶
- name = 'dw_tl_bulk_penalty'¶
- static stress_function(out, mat, det_f, vec_inv_cs)¶
- static tan_mod_function(out, mat, det_f, vec_inv_cs)¶
- class sfepy.terms.terms_hyperelastic_tl.BulkPressureTLTerm(*args, **kwargs)[source]¶
Hyperelastic bulk pressure term. Stress
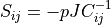 .
.- Definition:
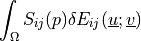
- Call signature:
dw_tl_bulk_pressure
(virtual, state, state_p)- Arguments:
virtual :

state :

state_p :

- arg_geometry_types = {('state_p', None): {'facet_extra': 'facet'}}¶
- arg_shapes = {'state': 'D', 'state_p': 1, 'virtual': ('D', 'state')}¶
- arg_types = ('virtual', 'state', 'state_p')¶
- family_data_names = ['det_f', 'sym_inv_c']¶
- get_eval_shape(virtual, state, state_p, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_tl_bulk_pressure'¶
- static stress_function(out, pressure_qp, det_f, vec_inv_cs)¶
- static tan_mod_u_function(out, pressure_qp, det_f, vec_inv_cs)¶
- static weak_dp_function(out, mtx_f, vec_inv_cs, det_f, cmap_s, cmap_v, transpose, mode)¶
- static weak_function(out, stress, tan_mod, mtx_f, det_f, cmap, is_diff, mode_ul)¶
- class sfepy.terms.terms_hyperelastic_tl.DiffusionTLTerm(*args, **kwargs)[source]¶
Diffusion term in the total Lagrangian formulation with linearized deformation-dependent permeability
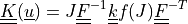 ,
where
,
where  relates to the previous time step
relates to the previous time step 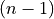 and
and
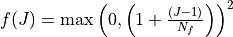 expresses the dependence on volume compression/expansion.
expresses the dependence on volume compression/expansion.- Definition:
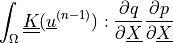
- Call signature:
dw_tl_diffusion
(material_1, material_2, virtual, state, parameter)- Arguments:
material_1 :
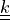
material_2 :
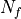
virtual :
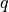
state :

parameter :
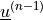
- arg_shapes = {'material_1': 'D, D', 'material_2': '1, 1', 'parameter': 'D', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('material_1', 'material_2', 'virtual', 'state', 'parameter')¶
- family_data_names = ['mtx_f', 'det_f']¶
- static function(out, pressure_grad, mtx_d, ref_porosity, mtx_f, det_f, cmap, mode)¶
- get_eval_shape(perm, ref_porosity, virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(perm, ref_porosity, virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_tl_diffusion'¶
- class sfepy.terms.terms_hyperelastic_tl.GenYeohTLTerm(*args, **kwargs)[source]¶
Hyperelastic generalized Yeoh term [1]. Effective stress
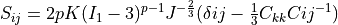 .
.- Definition:
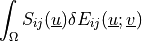
- Call signature:
dw_tl_he_genyeoh
(material, virtual, state)- Arguments:
material :
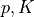
virtual :

state :

[1] Travis W. Hohenberger, Richard J. Windslow, Nicola M. Pugno, James J. C. Busfield. Aconstitutive Model For Both Lowand High Strain Nonlinearities In Highly Filled Elastomers And Implementation With User-Defined Material Subroutines In Abaqus. Rubber Chemistry And Technology, Vol. 92, No. 4, Pp. 653-686 (2019)
- arg_shapes = {'material': '1, 2', 'state': 'D', 'virtual': ('D', 'state')}¶
- family_data_names = ['det_f', 'tr_c', 'sym_inv_c']¶
- geometries = ['3_4', '3_8']¶
- name = 'dw_tl_he_genyeoh'¶
- class sfepy.terms.terms_hyperelastic_tl.HyperElasticSurfaceTLBase(*args, **kwargs)[source]¶
Base class for all hyperelastic surface terms in TL formulation family.
- get_family_data = HyperElasticSurfaceTLFamilyData¶
- class sfepy.terms.terms_hyperelastic_tl.HyperElasticSurfaceTLFamilyData(**kwargs)[source]¶
Family data for TL formulation applicable for surface terms.
- cache_name = 'tl_surface_common'¶
- data_names = ('mtx_f', 'det_f', 'inv_f')¶
- static family_function(mtx_f, det_f, mtx_fi, state, cmap, fis, conn)¶
- class sfepy.terms.terms_hyperelastic_tl.HyperElasticTLBase(*args, **kwargs)[source]¶
Base class for all hyperelastic terms in TL formulation family.
The subclasses should have the following static method attributes: - stress_function() (the stress) - tan_mod_function() (the tangent modulus)
The common (family) data are cached in the evaluate cache of state variable.
- get_family_data = HyperElasticTLFamilyData¶
- hyperelastic_mode = 0¶
- static weak_function(out, stress, tan_mod, mtx_f, det_f, cmap, is_diff, mode_ul)¶
- class sfepy.terms.terms_hyperelastic_tl.HyperElasticTLFamilyData(**kwargs)[source]¶
Family data for TL formulation.
- cache_name = 'tl_common'¶
- data_names = ('mtx_f', 'det_f', 'sym_c', 'tr_c', 'in2_c', 'sym_inv_c', 'green_strain')¶
- static family_function(mtx_f, det_f, vec_cs, tr_c, in_2c, vec_inv_cs, vec_es, state, cmap, conn)¶
- class sfepy.terms.terms_hyperelastic_tl.MooneyRivlinTLTerm(*args, **kwargs)[source]¶
Hyperelastic Mooney-Rivlin term. Effective stress
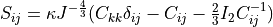 .
.- Definition:
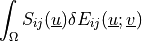
- Call signature:
dw_tl_he_mooney_rivlin
(material, virtual, state)- Arguments:
material :

virtual :

state :

- family_data_names = ['det_f', 'tr_c', 'sym_inv_c', 'sym_c', 'in2_c']¶
- name = 'dw_tl_he_mooney_rivlin'¶
- static stress_function(out, mat, det_f, tr_c, vec_inv_cs, vec_cs, in_2c)¶
- static tan_mod_function(out, mat, det_f, tr_c, vec_inv_cs, vec_cs, in_2c)¶
- class sfepy.terms.terms_hyperelastic_tl.NeoHookeanTLTerm(*args, **kwargs)[source]¶
Hyperelastic neo-Hookean term. Effective stress
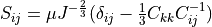 .
.- Definition:
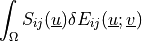
- Call signature:
dw_tl_he_neohook
(material, virtual, state)- Arguments:
material :
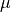
virtual :

state :

- family_data_names = ['det_f', 'tr_c', 'sym_inv_c']¶
- name = 'dw_tl_he_neohook'¶
- static stress_function(out, mat, det_f, tr_c, vec_inv_cs)¶
- static tan_mod_function(out, mat, det_f, tr_c, vec_inv_cs)¶
- class sfepy.terms.terms_hyperelastic_tl.OgdenTLTerm(*args, **kwargs)[source]¶
Single term of the hyperelastic Ogden model [1] with the strain energy density
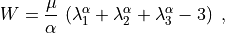
where
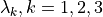 are the principal stretches, whose
squares are the principal values of the right Cauchy-Green deformation
tensor
are the principal stretches, whose
squares are the principal values of the right Cauchy-Green deformation
tensor  .
.Effective stress (2nd Piola-Kirchhoff) is [2]
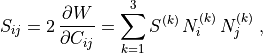
where the principal stresses are
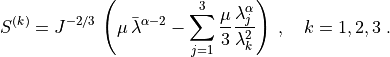
and
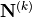 ,
, 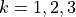 are the eigenvectors of
are the eigenvectors of
 .
.- Definition:
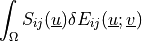
- Call signature:
dw_tl_he_ogden
(material, virtual, state)- Arguments:
material :
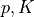
virtual :

state :

[1] Ogden, R. W. Large deformation isotropic elasticity - on the correlation of theory and experiment for incompressible rubberlike solids. Proceedings of the Royal Society A, Vol. 326, No. 1567, Pp. 565-584 (1972), DOI 10.1098/rspa.1972.0026.
[2] Steinmann, P., Hossain, M., Possart, G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Archive of Applied Mechanics, Vol. 82, No. 9, Pp. 1183-1217 (2012), DOI 10.1007/s00419-012-0610-z.
- arg_shapes = {'material': '1, 2', 'state': 'D', 'virtual': ('D', 'state')}¶
- family_data_names = ['det_f', 'sym_c', 'tr_c', 'sym_inv_c']¶
- geometries = ['3_4', '3_8']¶
- name = 'dw_tl_he_ogden'¶
- class sfepy.terms.terms_hyperelastic_tl.SurfaceFluxTLTerm(*args, **kwargs)[source]¶
Surface flux term in the total Lagrangian formulation, consistent with
DiffusionTLTerm.- Definition:
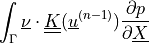
- Call signature:
ev_tl_surface_flux
(material_1, material_2, parameter_1, parameter_2)- Arguments:
material_1 :
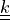
material_2 :
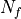
parameter_1 :

parameter_2 :
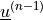
- arg_shapes = {'material_1': 'D, D', 'material_2': '1, 1', 'parameter_1': 1, 'parameter_2': 'D'}¶
- arg_types = ('material_1', 'material_2', 'parameter_1', 'parameter_2')¶
- family_data_names = ['det_f', 'inv_f']¶
- static function(out, pressure_grad, mtx_d, ref_porosity, mtx_fi, det_f, cmap, mode)¶
- get_eval_shape(perm, ref_porosity, pressure, displacement, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(perm, ref_porosity, pressure, displacement, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet_extra'¶
- name = 'ev_tl_surface_flux'¶
- class sfepy.terms.terms_hyperelastic_tl.SurfaceTractionTLTerm(*args, **kwargs)[source]¶
Surface traction term in the total Lagrangian formulation, expressed using
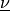 , the outward unit normal vector w.r.t. the
undeformed surface,
, the outward unit normal vector w.r.t. the
undeformed surface, 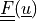 , the deformation gradient,
, the deformation gradient,
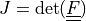 , and
, and 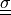 a given traction,
often equal to a given pressure, i.e.
a given traction,
often equal to a given pressure, i.e.
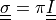 .
.- Definition:
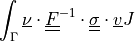
- Call signature:
dw_tl_surface_traction
(opt_material, virtual, state)- Arguments:
material :
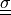
virtual :

state :

- arg_shapes = [{'opt_material': 'D, D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'virtual', 'state')¶
- family_data_names = ['det_f', 'inv_f']¶
- static function(out, traction, det_f, mtx_fi, bf, cmap, fis, mode)¶
- integration = 'facet_extra'¶
- name = 'dw_tl_surface_traction'¶
- class sfepy.terms.terms_hyperelastic_tl.VolumeSurfaceTLTerm(*args, **kwargs)[source]¶
Volume of a
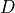 -dimensional domain, using a surface integral in the
total Lagrangian formulation, expressed using
-dimensional domain, using a surface integral in the
total Lagrangian formulation, expressed using 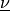 , the outward
unit normal vector w.r.t. the undeformed surface,
, the outward
unit normal vector w.r.t. the undeformed surface, 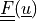 ,
the deformation gradient, and
,
the deformation gradient, and 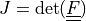 . Uses the
approximation of
. Uses the
approximation of  for the deformed surface coordinates
for the deformed surface coordinates
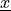 .
.- Definition:
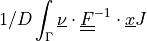
- Call signature:
ev_tl_volume_surface
(parameter)- Arguments:
parameter :

- arg_shapes = {'parameter': 'D'}¶
- arg_types = ('parameter',)¶
- family_data_names = ['det_f', 'inv_f']¶
- static function(out, coors, det_f, mtx_fi, bf, cmap, conn)¶
- integration = 'facet_extra'¶
- name = 'ev_tl_volume_surface'¶
- class sfepy.terms.terms_hyperelastic_tl.VolumeTLTerm(*args, **kwargs)[source]¶
Volume term (weak form) in the total Lagrangian formulation.
- Definition:
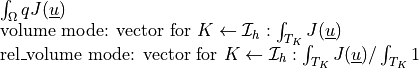
- Call signature:
dw_tl_volume
(virtual, state)- Arguments:
virtual :
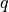
state :

- arg_geometry_types = {('virtual', None): {'facet_extra': 'facet'}}¶
- arg_shapes = {'state': 'D', 'virtual': (1, None)}¶
- arg_types = ('virtual', 'state')¶
- family_data_names = ['mtx_f', 'det_f', 'sym_inv_c']¶
- static function(out, mtx_f, vec_inv_cs, det_f, cmap_s, cmap_v, transpose, mode)¶
- name = 'dw_tl_volume'¶