sfepy.terms.terms_dg module¶
Discontinous Galekrin method specific terms
Note¶
In einsum calls the following convention is used:
i represents iterating over all cells of a region;
n represents iterating over selected cells of a region, for example over cells on boundary;
b represents iterating over basis functions of state variable;
d represents iterating over basis functions of test variable;
k, l , m represent iterating over geometric dimensions, for example coordinates of velocity or facet normal vector or rows and columns of diffusion tensor;
q represents iterating over quadrature points;
f represents iterating over facets of cell;
- class sfepy.terms.terms_dg.AdvectionDGFluxTerm(name, arg_str, integral, region, **kwargs)[source]¶
Lax-Friedrichs flux term for advection of scalar quantity
 with the
advection velocity
with the
advection velocity 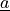 given as a material parameter (a known
function of space and time).
given as a material parameter (a known
function of space and time).- Definition:
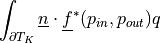
where
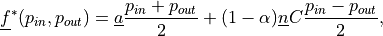
![\alpha \in [0, 1]](../../../_images/math/365312130995f6781a5dacc5da0d387c92a09efc.png) ;
; 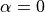 for upwind scheme,
for upwind scheme,
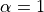 for central scheme, and
for central scheme, and![C = \max_{p \in [?, ?]}\left\lvert n_x a_1 +
n_y a_2 \right\rvert =
\max_{p \in [?, ?]} \left\lvert \ul{n} \cdot \ul{a} \right\rvert](../../../_images/math/42d3f6efba4277b5178cb35ebd3eda7e4679f24b.png)
the
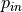 resp.
resp. 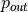 is solution on the boundary of the element
provided by element itself resp. its
neighbor and
is solution on the boundary of the element
provided by element itself resp. its
neighbor and 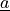 is advection velocity.
is advection velocity.- Call signature:
dw_dg_advect_laxfrie_flux
(opt_material, material_advelo, virtual, state)- Arguments 1:
material :
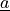
virtual :
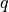
state :

- Arguments 3:
material :
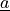
virtual :
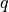
state :

opt_material :
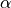
- alpha = 0¶
- arg_shapes = [{'material_advelo': 'D, 1', 'opt_material': '.: 1', 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'material_advelo', 'virtual', 'state')¶
- integration = 'cell'¶
- modes = ('weak',)¶
- name = 'dw_dg_advect_laxfrie_flux'¶
- symbolic = {'expression': 'div(a*p)*w', 'map': {'a': 'material', 'p': 'state', 'v': 'virtual'}}¶
- class sfepy.terms.terms_dg.DGTerm(name, arg_str, integral, region, **kwargs)[source]¶
Abstract base class for DG terms, provides alternative call_function and eval_real methods to accommodate returning iels and vals.
- poly_space_basis = 'legendre'¶
- class sfepy.terms.terms_dg.DiffusionDGFluxTerm(name, arg_str, integral, region, **kwargs)[source]¶
Basic DG diffusion flux term for scalar quantity.
- Definition:
![\int_{\partial{T_K}} D \langle \nabla p \rangle [q] \mbox{ , }
\int_{\partial{T_K}} D \langle \nabla q \rangle [p]](../../../_images/math/8adae2ce0c1763d5d157c62288772d6f2e9d82ab.png)
where
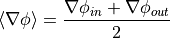
![[\phi] = \phi_{in} - \phi_{out}](../../../_images/math/93f3b2071ecd9b131f2fd0d22b4c2801b4b86a5f.png)
- Math:
The
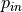 resp.
resp. 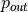 is solution on the boundary of the element
provided by element itself resp. its neighbour.
is solution on the boundary of the element
provided by element itself resp. its neighbour.- Call signature:
dw_dg_diffusion_flux
(material, state, virtual)(material, virtual, state)- Arguments 1:
material :
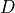
state :

virtual :
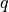
- Arguments 2:
material :
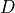
virtual :
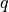
state :

- arg_shapes = [{'material': '1, 1', 'state/avg_state': 1, 'state/avg_virtual': 1, 'virtual/avg_state': (1, None), 'virtual/avg_virtual': (1, None)}]¶
- arg_types = (('material', 'state', 'virtual'), ('material', 'virtual', 'state'))¶
- integration = 'cell'¶
- modes = ('avg_state', 'avg_virtual')¶
- name = 'dw_dg_diffusion_flux'¶
- class sfepy.terms.terms_dg.DiffusionInteriorPenaltyTerm(name, arg_str, integral, region, **kwargs)[source]¶
Penalty term used to counteract discontinuity arising when modeling diffusion using Discontinuous Galerkin schemes.
- Definition:
![\int_{\partial{T_K}} \bar{D} C_w \frac{Ord^2}{d(\partial{T_K})}[p][q]](../../../_images/math/9f27ae98f2604e8ba1d4bbf684e11292c3e2997c.png)
where
![[\phi] = \phi_{in} - \phi_{out}](../../../_images/math/93f3b2071ecd9b131f2fd0d22b4c2801b4b86a5f.png)
- Math:
the
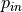 resp.
resp. 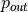 is solution on the boundary of the element
provided by element itself resp. its neighbour.
is solution on the boundary of the element
provided by element itself resp. its neighbour.- Call signature:
dw_dg_interior_penalty
(material, material_Cw, virtual, state)- Arguments:
material :
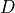
material :
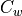
state :

virtual :
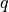
- arg_shapes = [{'material': '1, 1', 'material_Cw': '.: 1', 'state': 1, 'virtual': (1, 'state')}]¶
- arg_types = ('material', 'material_Cw', 'virtual', 'state')¶
- get_fargs(diff_tensor, Cw, test, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- modes = ('weak',)¶
- name = 'dw_dg_interior_penalty'¶
- class sfepy.terms.terms_dg.NonlinearHyperbolicDGFluxTerm(name, arg_str, integral, region, **kwargs)[source]¶
Lax-Friedrichs flux term for nonlinear hyperpolic term of scalar quantity
 with the vector function
with the vector function 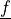 given as a material
parameter.
given as a material
parameter.- Definition:
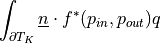
where
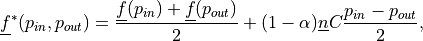
![\alpha \in [0, 1]](../../../_images/math/365312130995f6781a5dacc5da0d387c92a09efc.png) ;
; 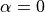 for upwind scheme,
for upwind scheme,
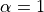 for central scheme, and
for central scheme, and![C =
\max_{p \in [?, ?]}\left\lvert
n_x \frac{d f_1}{d p} + n_y \frac{d f_2}{d p}
+ \cdots
\right\rvert =
\max_{p \in [?, ?]} \left\lvert
\vec{n}\cdot\frac{d\ul{f}}{dp}(p)
\right\rvert](../../../_images/math/cdff00b7b3fe5ac5a18a9582f189e875bdeaa16e.png)
the
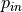 resp.
resp. 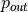 is solution on the boundary of the element
provided by element itself resp. its
neighbor.
is solution on the boundary of the element
provided by element itself resp. its
neighbor.- Call signature:
dw_dg_nonlinear_laxfrie_flux
(opt_material, fun, fun_d, virtual, state)- Arguments 1:
material :
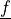
material :
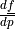
virtual :
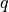
state :

- Arguments 3:
material :
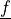
material :
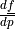
virtual :
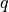
state :

opt_material :
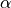
- alf = 0¶
- arg_shapes = [{'material_fun': '.: 1', 'material_fun_d': '.: 1', 'opt_material': '.: 1', 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'fun', 'fun_d', 'virtual', 'state')¶
- get_fargs(alpha, fun, dfun, test, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'cell'¶
- modes = ('weak',)¶
- name = 'dw_dg_nonlinear_laxfrie_flux'¶
- symbolic = {'expression': 'div(f(p))*w', 'map': {'f': 'function', 'p': 'state', 'v': 'virtual'}}¶
- class sfepy.terms.terms_dg.NonlinearScalarDotGradTerm(name, arg_str, integral, region, **kwargs)[source]¶
Product of virtual and divergence of vector function of state or volume dot product of vector function of state and gradient of scalar virtual.
- Definition:
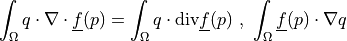
- Call signature:
dw_ns_dot_grad_s
(fun, fun_d, virtual, state)(fun, fun_d, state, virtual)- Arguments 1:
function :
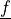
virtual :
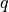
state :

- Arguments 2:
function :
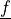
state :

virtual :
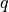
TODO maybe this term would fit better to terms_dot?
- arg_shapes = [{'material_fun': '.: 1', 'material_fun_d': '.: 1', 'state/grad_state': 1, 'state/grad_virtual': 1, 'virtual/grad_state': (1, None), 'virtual/grad_virtual': (1, None)}]¶
- arg_types = (('fun', 'fun_d', 'virtual', 'state'), ('fun', 'fun_d', 'state', 'virtual'))¶
- modes = ('grad_state', 'grad_virtual')¶
- name = 'dw_ns_dot_grad_s'¶