sfepy.linalg.geometry module¶
- sfepy.linalg.geometry.barycentric_coors(coors, s_coors)[source]¶
Get barycentric (area in 2D, volume in 3D) coordinates of points with coordinates coors w.r.t. the simplex given by s_coors.
- Returns:
- bcarray
The barycentric coordinates. Then reference element coordinates xi = dot(bc.T, ref_coors).
- sfepy.linalg.geometry.flag_points_in_polygon2d(polygon, coors)[source]¶
Test if points are in a 2D polygon.
- Parameters:
- polygonarray, (:, 2)
The polygon coordinates.
- coors: array, (:, 2)
The coordinates of points.
- Returns:
- flagbool array
The flag that is True for points that are in the polygon.
Notes
This is a semi-vectorized version of [1].
[1] PNPOLY - Point Inclusion in Polygon Test, W. Randolph Franklin (WRF)
- sfepy.linalg.geometry.get_coors_in_ball(coors, centre, radius, radius2=None, inside=True)[source]¶
Return indices of coordinates inside or outside a ball given by centre and radius:
inside radius radius2 condition True r None |x - c| <= r True r r2 r2 <= |x - c| <= r False r None |x - c| >= r False r r2 |x - c| >= r | |x - c| <= r2
Notes
All float comparisons are done using <= or >= operators, i.e. the points on the boundaries are taken into account.
- sfepy.linalg.geometry.get_coors_in_tube(coors, centre, axis, radius_in, radius_out, length, inside_radii=True)[source]¶
Return indices of coordinates inside a tube given by centre, axis vector, inner and outer radii and length.
- Parameters:
- inside_radiibool, optional
If False, select points outside the radii, but within the tube length.
Notes
All float comparisons are done using <= or >= operators, i.e. the points on the boundaries are taken into account.
- sfepy.linalg.geometry.get_face_areas(faces, coors)[source]¶
Get areas of planar convex faces in 2D and 3D.
- Parameters:
- facesarray, shape (n, m)
The indices of n faces with m vertices into coors.
- coorsarray
The coordinates of face vertices.
- Returns:
- areasarray
The areas of the faces.
- sfepy.linalg.geometry.get_perpendiculars(vec)[source]¶
For a given vector, get a unit vector perpendicular to it in 2D, or get two mutually perpendicular unit vectors perpendicular to it in 3D.
- sfepy.linalg.geometry.get_simplex_circumcentres(coors, force_inside_eps=None)[source]¶
Compute the circumcentres of n_s simplices in 1D, 2D and 3D.
- Parameters:
- coorsarray
The coordinates of the simplices with n_v vertices given in an array of shape (n_s, n_v, dim), where dim is the space dimension and 2 <= n_v <= (dim + 1).
- force_inside_epsfloat, optional
If not None, move the circumcentres that are outside of their simplices or closer to their boundary then force_inside_eps so that they are inside the simplices at the distance given by force_inside_eps. It is ignored for edges.
- Returns:
- centresarray
The circumcentre coordinates as an array of shape (n_s, dim).
- sfepy.linalg.geometry.get_simplex_volumes(cells, coors)[source]¶
Get volumes of simplices in nD.
- Parameters:
- cellsarray, shape (n, d)
The indices of n simplices with d vertices into coors.
- coorsarray
The coordinates of simplex vertices.
- Returns:
- volumesarray
The volumes of the simplices.
- sfepy.linalg.geometry.inverse_element_mapping(coors, e_coors, eval_basis, ref_coors, suppress_errors=False)[source]¶
Given spatial element coordinates, find the inverse mapping for points with coordinats X = X(xi), i.e. xi = xi(X).
- Returns:
- xiarray
The reference element coordinates.
- sfepy.linalg.geometry.make_axis_rotation_matrix(direction, angle)[source]¶
Create a rotation matrix
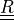 corresponding to the
rotation around a general axis
corresponding to the
rotation around a general axis 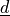 by a specified angle
by a specified angle
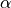 .
.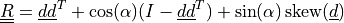
- Parameters:
- directionarray
The rotation axis direction vector
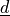 .
.- anglefloat
The rotation angle
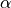 .
.
- Returns:
- mtxarray
The rotation matrix
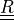 .
.
Notes
The matrix follows the right hand rule: if the right hand thumb points along the axis vector
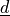 the fingers show the
positive angle rotation direction.
the fingers show the
positive angle rotation direction.Examples
Make transformation matrix for rotation of coordinate system by 90 degrees around ‘z’ axis.
>>> mtx = make_axis_rotation_matrix([0., 0., 1.], nm.pi/2) >>> mtx array([[ 0., 1., 0.], [-1., 0., 0.], [ 0., 0., 1.]])
Coordinates of vector
![[1, 0, 0]^T](../../../_images/math/f13290a320b67f99ccf8b50478ccc7877dcd1b55.png) w.r.t. the original system
in the rotated system. (Or rotation of the vector by -90 degrees in
the original system.)
w.r.t. the original system
in the rotated system. (Or rotation of the vector by -90 degrees in
the original system.)>>> nm.dot(mtx, [1., 0., 0.]) >>> array([ 0., -1., 0.])
Coordinates of vector
![[1, 0, 0]^T](../../../_images/math/f13290a320b67f99ccf8b50478ccc7877dcd1b55.png) w.r.t. the rotated system
in the original system. (Or rotation of the vector by +90 degrees in
the original system.)
w.r.t. the rotated system
in the original system. (Or rotation of the vector by +90 degrees in
the original system.)>>> nm.dot(mtx.T, [1., 0., 0.]) >>> array([ 0., 1., 0.])
- sfepy.linalg.geometry.points_in_simplex(coors, s_coors, eps=1e-08)[source]¶
Test if points with coordinates coors are in the simplex given by s_coors.