Homogenization of peristaltic flows in piezoelectric porous media

Model

This example shows the numerical implementation of the homogenized problem of peristaltic flow in porous piezoelectric materials saturated by electrically inert fluid. The solid part of a representative volume element consists of the piezoelectric skeleton with embedded conductors. The pore fluid in the periodic structure constitutes a single connected domain. The electrodes control the electric field at the pore level, so that the peristaltic wave of the deformation influences the pore volume and can control the direction of fluid flow. For details, see [RohanLukes2023].

Implementation

The homogenized coefficients, their sensitivities, and the microscopic subproblems are defined in poropiezo_micro.py and poropiezo_micro_sa.py. The periodic reference cell, on which the microscopic subproblems are solved, is depicted in Fig. 1. The FE mesh of the reference cell is stored in mesh_micro_1D.vtk.

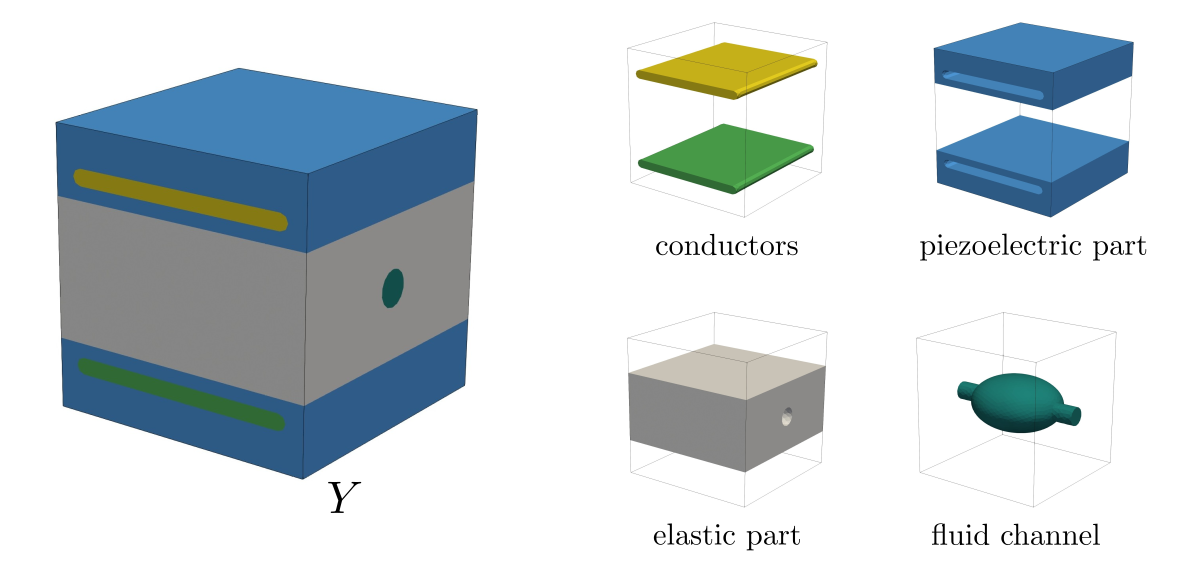
Fig. 1 Decomposition of the microscopic reference cell.

The problem description file coding the homogenized macroscopic equations invokes poropiezo_macro_nl.py. The FE mesh related to the macroproblem is defined in mesh_macro_20x1x1.vtk. The applied boundary conditions are shown in Fig. 2, and the prescribed electric potential, inducing the deformation and thus the fluid flow through the structure, is depicted in Fig. 3.

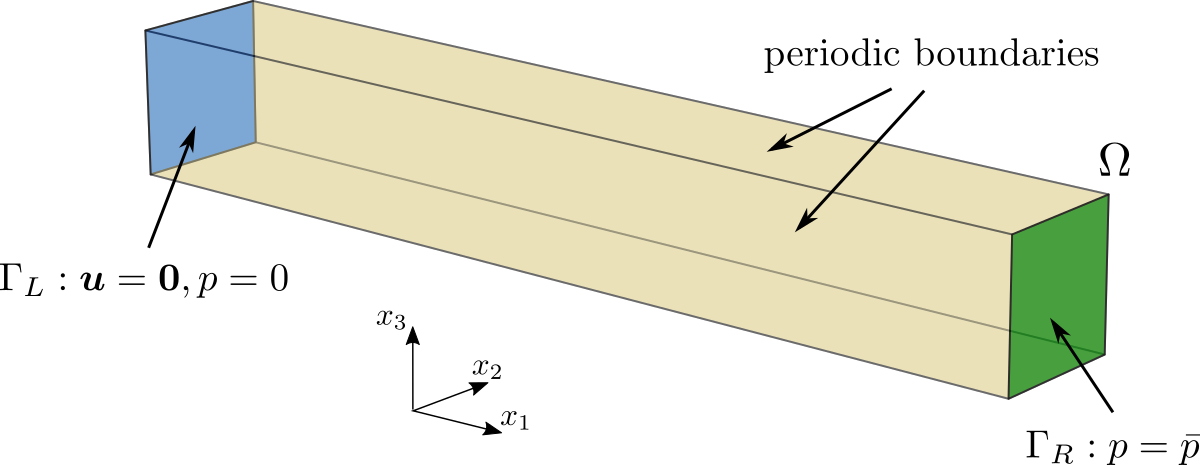
Fig. 2 Boundary conditions applied to the macroscopic sample.

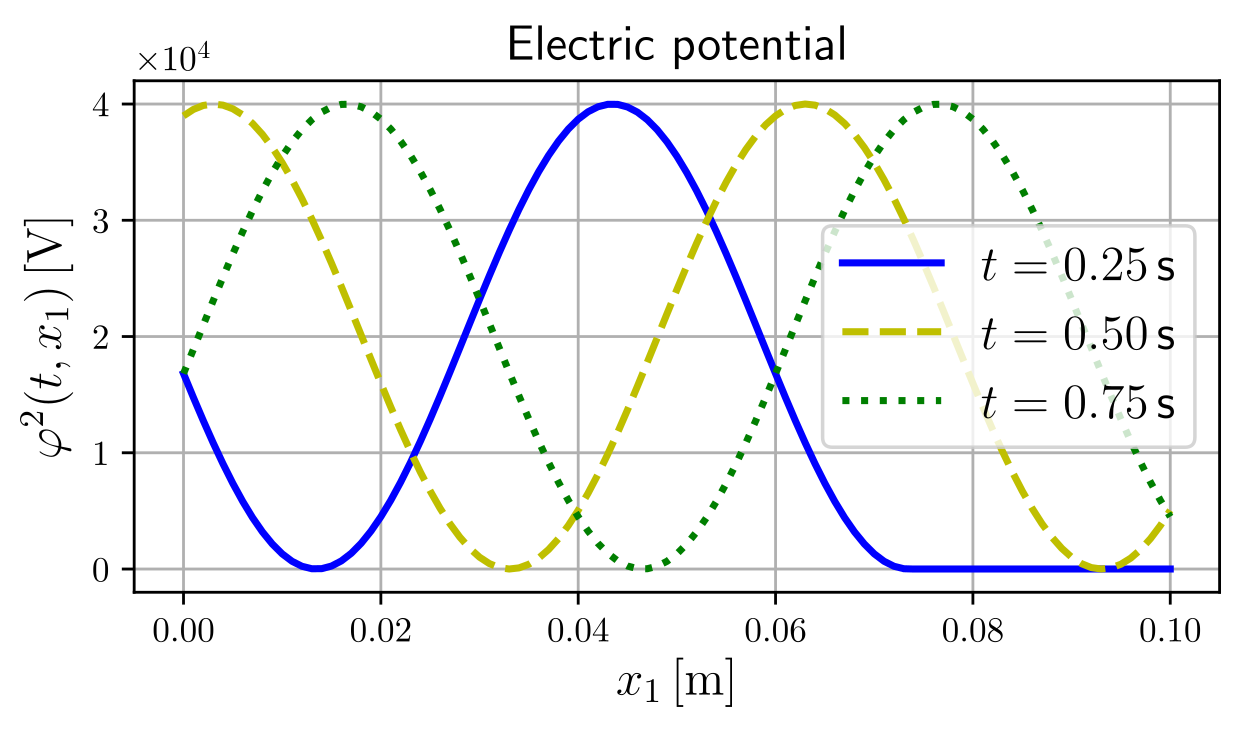
Fig. 3 Electric potential at selected times.

Running simulation

To run the multiscale numerical simulation, download the archive, unpack it and type:

sfepy-run example_piezo_flow-1/piezo_macro_nl.py

In the first step, SfePy invokes the homogenization engine, see [CimrmanLukesRohan2019], which solves the microscopic subproblems and evaluates the homogenized coefficients required at the macroscopic level. In the second step, the time-stepping solver resolves the macroscopic problem for given boundary conditions, and the reconstruction of the displacement, pressure, and velocity fields at the microscopic level is performed.

The reconstructed pressure and velocity fields are shown in Fig. 4.

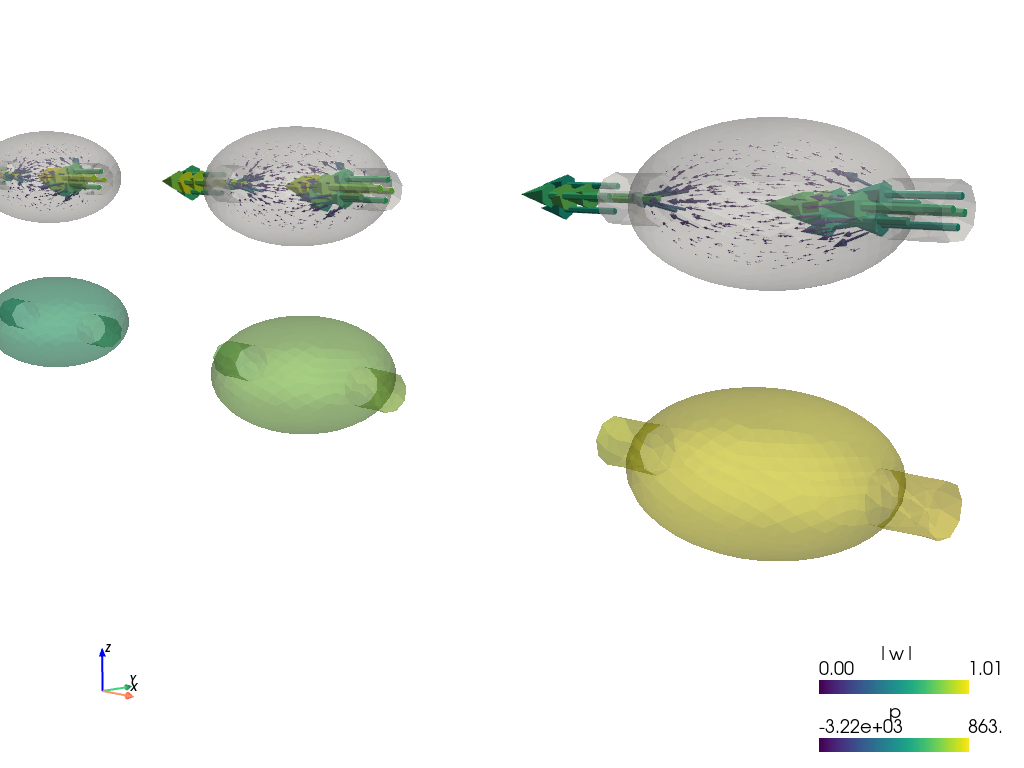
Fig. 4 Reconstructed pressure and velocity fields at a given time step.

The above figure was generated by the post-processing script as follows:

sfepy-view output/mesh_micro_1D.recovered_0.001.040_Yf.vtk -f p:o.4:p0 w:g:f5e-4:p1 0:o.4:p1 --camera-position="0.101136,-0.0016623,0.00179498,0.0917673,0.00652579,-0.000337183,-0.1227,0.116262,0.98561"

This simulation demonstrates the ability of the porose piezoelectric structure to transport fluid against the pressure drop given by the prescribed boundary pressures. The dependence of the transported fluid on the magnitude of the electrical potential is depicted in Fig. 5.

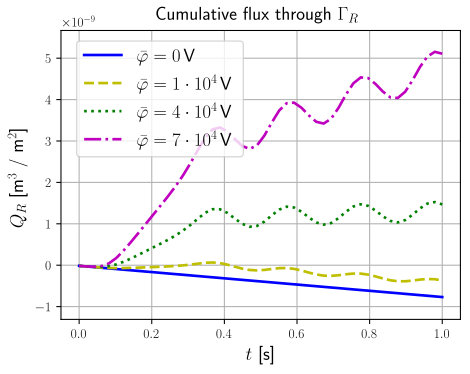
Fig. 5 Dependence of cumulative flux on the amplitude of the prescribed electric potential.

References

RohanLukes2023

Rohan E., Lukeš V. Homogenization of peristaltic flows in piezoelectric porous media. Preprint arXiv:2304.05393, 2023, DOI: 10.48550/arXiv.2304.05393

CimrmanLukesRohan2019

Cimrman R., Lukeš V., Rohan E. Multiscale finite element calculations in Python using SfePy. Advances in Computational Mathematics, 45(4):1897-1921, 2019, DOI:10.1007/s10444-019-09666-0