User’s Guide¶
The purpose of this software is to predict distribution of acoustic band gaps in phononic materials in 2D and 3D.
Introduction¶
We will briefly recall the notions of a phononic material and acoustic band gaps using the piezoelastic material. The purely elastic case is its special simplified version.
For a more complete description involving details of application of the theory of homogenization, see e.g. [rohan-miara-seifrt-2009].
Strongly heterogeneous material¶
The material properties are related to the periodic geometrical decomposition like in Fig. Periodic structure of the piezoelectric composite with -scaled material in the inclusions ..
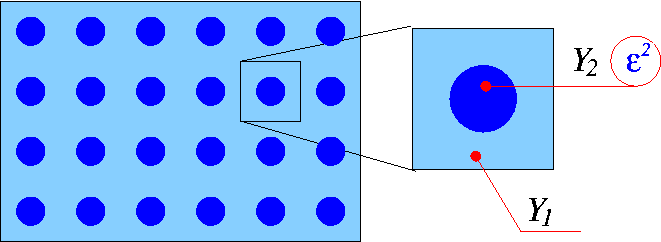
Periodic structure of the piezoelectric composite with
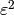 -scaled material in the inclusions
-scaled material in the inclusions 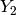 .
.
Properties of a piezoelectric material are described by three tensors: the
elasticity tensor 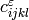 , the dielectric tensor
, the dielectric tensor
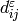 and the piezoelectric coupling tensor
and the piezoelectric coupling tensor
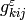 , where
, where 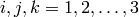 .
.
We assume that inclusions are occupied by a very soft material in such a
sense that there the material coefficients are significantly smaller than those
of the matrix compartment, except the material density, which is comparable
in both the compartments; as an important feature of the modelling, the strong
heterogeneity is related to the geometrical scale of the underlying
microstructure by coefficient 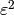 :
:
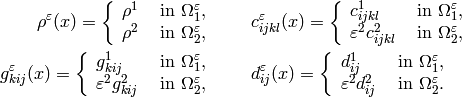
Problem formulation¶
We consider a stationary wave propagation in the medium introduced above. For
simplicity we restrict the model to the description of clamped structures
loaded by volume forces and subject to volume distributed electric charges.
For a synchronous harmonic excitation of a single frequency 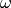
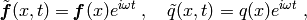
where 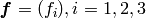 is the magnitude field of the applied volume
force and
is the magnitude field of the applied volume
force and 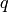 is the magnitude of the distributed volume charge, we have
in general a dispersive piezoelectric field with magnitudes
is the magnitude of the distributed volume charge, we have
in general a dispersive piezoelectric field with magnitudes
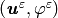

This allows us to study the steady periodic response of the medium, as
characterized by fields 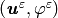 which satisfy the
following boundary value problem:
which satisfy the
following boundary value problem:

where the stress tensor 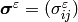 and the
electric displacement
and the
electric displacement 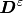 are defined by constitutive laws
are defined by constitutive laws
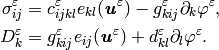
The problem eq{eq-11} can be weakly formulated as follows: Find
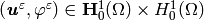 such that
such that
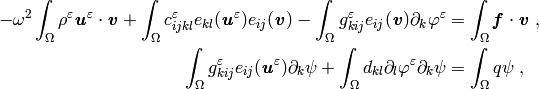
for all 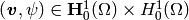 , where
, where 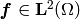 ,
, 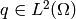 .
.
Spectral problem¶
Let us denote
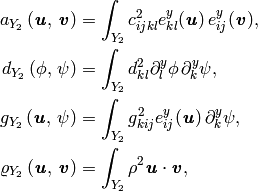
whereby analogical notation is used when integrating over 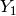 .
.
The spectral problem reads as: find eigenelements ![[\lam^r;
(\zb^r,p^r)]](_images/math/78f15ceef39fe28e557565f04a60695b19eb1dab.png) , where
, where 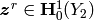 and
and 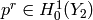 ,
, 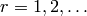 , such that
, such that
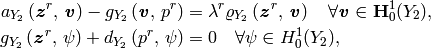
with the orthonormality condition imposed on eigenfunctions 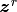 :
:
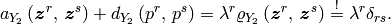
Homogenized coefficients¶
The macroscopic model of elastic waves in strongly heterogeneous piezoelectric composite involves two groups of the homogenized material coefficients:
- the homogenized coefficients depending on the incident wave frequency - these are responsible for the dispersive properties of the homogenized model. This group of the coefficients depends just on the material properties of the inclusion (except the material density, which is averaged over entire
)
- the second group of coefficients is related exclusively to the matrix compartment – it determines the macroscopic piezo-elastic properties.
Let us summarize just the first group of coefficients, as those are connected with the appearance of the band gaps.
We introduce the eigenmomentum 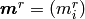 ,
,
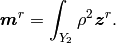
Then the following tensors are introduced, all depending on 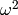 :
- Mass tensor
:
- Mass tensor 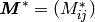
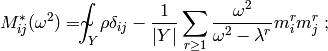
- Applied load tensor
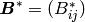
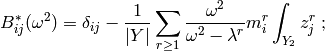
- Applied charge tensor
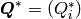
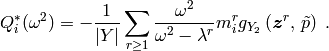
Band gaps¶
The band gaps are frequency intervals for which the propagation of waves in the structure is disabled or restricted in the polarization.
The band gaps can be classified w.r.t. the polarization of waves which cannot
propagate. Given a frequency 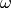 , there are three cases to be
distinguished according to the signs of eigenvalues
, there are three cases to be
distinguished according to the signs of eigenvalues 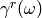 ,
,
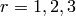 (in 3D), which determine the ``positivity, or negativity’’ of
the mass:
(in 3D), which determine the ``positivity, or negativity’’ of
the mass:
- {bf propagation zone} – all eigenvalues of
are positive: then homogenized model eq{eq-45s} admits wave propagation without any restriction of the wave polarization;
- {bf strong band gap} – all eigenvalues of
are negative: then homogenized model eq{eq-45s} does {it not} admit any wave propagation;
- {bf weak band gap} – tensor
is indefinite, i.e. there is at least one negative and one positive eigenvalue: then propagation is possible only for waves polarized in a manifold determined by eigenvectors associated with positive eigenvalues. In this case the notion of wave propagation has a local character, since the ``desired wave polarization’’ may depend on the local position in
.
In Fig. Distribution of the band gaps. we illustrate weak band gap distribution for piezoelectric composite formed by matrix PZT5A with embedded spherical inclusions made of BaTiOx3.
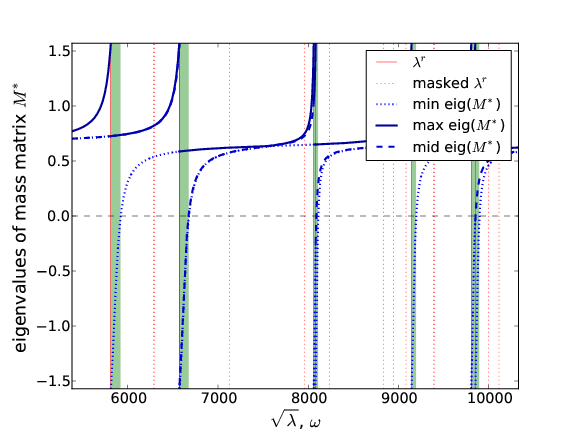
Distribution of the band gaps.
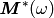 .
.The software can also perform dispersion analysis of long guided waves, a example result is shown in Fig. The dispersion analysis..
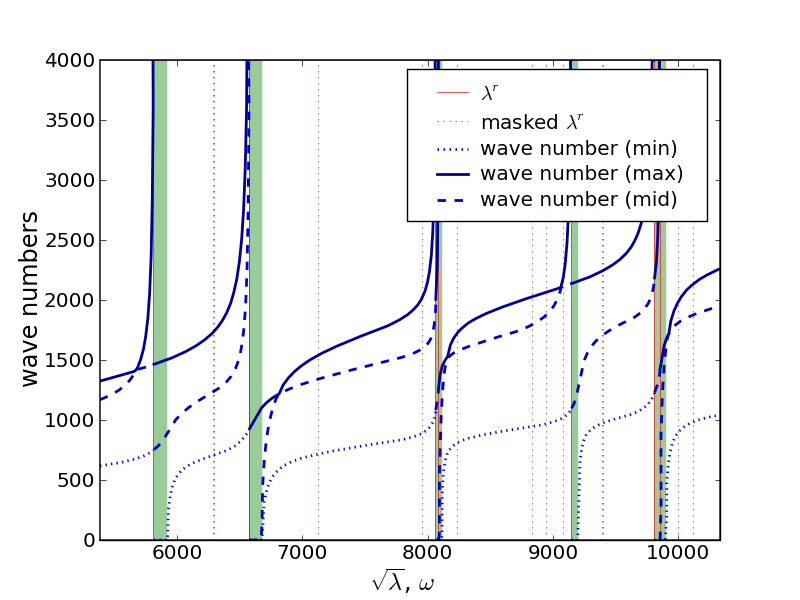
The dispersion analysis.
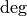 . In the weak band gaps
(grey/green strips) analyzed according to Fig. Distribution of the band gaps. waves
can propagate in one or two directions only. In the second band gap only
one polarization exists, with the phase velocity determined by the blue
(solid) curve, in the first band gap two polarizations can propagate. In
the ``full propagation zones’’ (white) the three curves correspond to the
three wave polarizations.}
. In the weak band gaps
(grey/green strips) analyzed according to Fig. Distribution of the band gaps. waves
can propagate in one or two directions only. In the second band gap only
one polarization exists, with the phase velocity determined by the blue
(solid) curve, in the first band gap two polarizations can propagate. In
the ``full propagation zones’’ (white) the three curves correspond to the
three wave polarizations.}References¶
| [rohan-miara-seifrt-2009] | Rohan, E., Miara, B. and Seifrt, F., 2009. Numerical simulation of acoustic band gaps in homogenized elastic compo sites. International Journal of Engineering Science. 4(47):573-594. doi://10.1016/j.ijengsci.2008.12.003. |
Running a simulation¶
The band gap related problems can be solved by running the eigen.py script:
Usage: eigen.py [options] filename_in
Options:
--version show program's version number and exit
-h, --help show this help message and exit
-o filename basename of output file(s) [default: <basename of input
file>]
-b, --band-gaps detect frequency band gaps
-d, --dispersion analyze dispersion properties (low frequency domain)
-p, --plot plot frequency band gaps, assumes -b
--phase-velocity compute phase velocity (frequency-independet mass only)
Above filename_in stands for one of the problem definition files listed below. Each of the files contains all the necessary information to compute acoustic band gaps (ABG) and/or dispersion properties (DP) , namely:
- band_gaps.py (ABG + DP in elastic material)
- band_gaps_liquid.py (ABG in elastic material with fluid-like inclusion)
- band_gaps_piezo.py (ABG + DP in piezoelastic material)
- band_gaps_rigid.py (ABG in elastic material with rigid inclusion)
Each of the above files includes further options, that can be set to influence both the computation and subsequent postprocessing of results (accuracy settings, names and format of result files etc.).
Postprocessing¶
Results of a simulation are:
- graphical representation of ABG and eventually DP; the figure are saved to the directory specified in options of each problem definition file,
- text file of ABG, DP logs for custom postprocessing using plot_gaps.py script,
- eigenfunctions of the related elasticity or piezoelasticity eigenvalue problems in the standard VTK format or a custom HDF5-based format, eigenvalues in text files.